题目内容
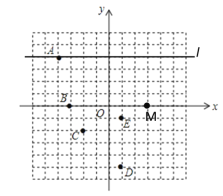
【题目】在平面直角坐标系中，
的顶点都在网格的格点上（如图所示）．
（1）写出点
的坐标____________，且该点到
轴的距离为__________．
（2）作关于轴的轴对称图形
．
（3）判断的形状，并说明理由．
【答案】（1）
；1；（2）作图见详解；（3）
是等腰直角三角形，理由见详解
【解析】
（1）根据点的位置即可写出坐标，点
横坐标的绝对值即为该点到
轴的距离；
（2）根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”分别作出
关于y轴对称的点
，再顺次连接即可；
（3）运用勾股定理分别求出的三边长，可得有两边相等，再运用勾股定理的逆定理证明是直角三角形，即可判断三角形的形状.
解：（1）由图可读出：，
∵点横坐标的绝对值即为该点到轴的距离；
∴点到轴的距离为1；
故答案为：；1.
（2）如下图，
即为所作图形．
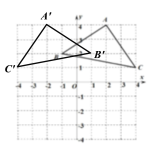
（3）是等腰直角三角形，理由如下：
根据勾股定理即可得到：
，
，
，
∴
，
，
∴
，
∴是直角三角形，且
，
又∵，
∴是等腰直角三角形.
练习册系列答案
相关题目
