题目内容
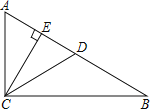
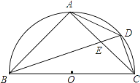
【题目】如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC= ![]() ,CD=
,CD= ![]() ,则sin∠AEB的值为________.
,则sin∠AEB的值为________.
【答案】![]() .
.
【解析】
试题在△ABE与△DBC中,有∠ABE=∠DBC,∠BAE=∠BDC=90°,得到△ABE∽△DBC,可知∠AEB=∠DCB,在Rt△DCB中,先由勾股定理求出BD的值,再根据正弦的定义求出sin∠DCB,得出sin∠AEB的值.
解:∵BC为半圆的直径,
∴∠BAE=∠BDC=90°.
∵D是弧AC的中点,
∴∠ABE=∠DBC.
∴△ABE∽△DBC.
在RT△DCB中,
∵∠BDC=90°,BC=![]() ,CD=
,CD=![]() ,
,
∴BD=![]() ,
,
∴sin∠DCB=BD:BC=![]() ,
,
∵△ABE∽△DBC,
∴∠AEB=∠DCB.
∴sin∠AEB=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
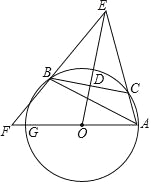
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.