题目内容
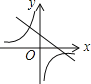
【题目】已知二次函数y=﹣![]() x2+bx+c的图象经过A(0,3),B(﹣4,﹣
x2+bx+c的图象经过A(0,3),B(﹣4,﹣![]() )两点.
)两点.
(1)求b,c的值.
(2)二次函数y=﹣![]() x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.
x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.
【答案】(1)![]() ;(2)公共点的坐标是(﹣2,0)或(8,0).
;(2)公共点的坐标是(﹣2,0)或(8,0).
【解析】(1)把点A、B的坐标分别代入函数解析式求得b、c的值;
(2)利用根的判别式进行判断该函数图象是否与x轴有交点,由题意得到方程﹣![]() +3=0,通过解该方程求得x的值即为抛物线与x轴交点横坐标.
+3=0,通过解该方程求得x的值即为抛物线与x轴交点横坐标.
(1)把A(0,3),B(﹣4,﹣![]() )分别代入y=﹣
)分别代入y=﹣![]() x2+bx+c,
x2+bx+c,
得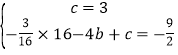 ,
,
解得![]() ;
;
(2)由(1)可得,该抛物线解析式为:y=﹣![]() x2+
x2+![]() x+3,
x+3,
△=(![]() )2﹣4×(﹣
)2﹣4×(﹣![]() )×3=
)×3=![]() >0,
>0,
所以二次函数y=﹣![]() x2+bx+c的图象与x轴有公共点,
x2+bx+c的图象与x轴有公共点,
∵﹣![]() x2+
x2+![]() x+3=0的解为:x1=﹣2,x2=8,
x+3=0的解为:x1=﹣2,x2=8,
∴公共点的坐标是(﹣2,0)或(8,0).

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目