题目内容
【题目】如图,长方形ABCD中,AB=8,BC=12,点E是边BC上一点,BE=5,点F是射线BA上一动点,连接EF,将△BEF沿着EF折叠,使B点的对应点P落在长方形一边的垂直平分线上,连接BP,则BP的长是_____.

【答案】4![]() 或
或![]() 或2
或2![]()
【解析】
分三种情况:①当P落在AB边的垂直平分线上且F在BA的延长线上时;②当P落在AB边的垂直平分线上且F在BA上时;③当P落在BC边的垂直平分线上时;由折叠的性质和勾股定理即可得出答案.
解:分三种情况:①当P落在AB边的垂直平分线上时,如图1所示:
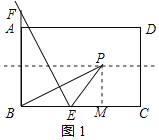
作PM⊥BC于M,则PM=![]() AB=4,∠PMB=90°,
AB=4,∠PMB=90°,
由折叠的性质得:PE=BE=5,
∴EM=![]() =3,
=3,
∴BM=BE+EM=8,
∴BP=![]() ;
;
②当P落在AB边的垂直平分线上,且F在线段BA上时,如图2所示:
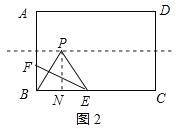
作PN⊥BC于N,则PN=![]() AB=4,∠PNB=90°,
AB=4,∠PNB=90°,
由折叠的性质得:PE=BE=5,
∴EN=![]() =3,
=3,
∴BN=BE-EN=2,
∴BP=![]() ;
;
③当P落在BC边的垂直平分线上时,如图3所示:
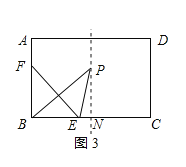
则BN=![]() BC=6,∠PNB=90°,
BC=6,∠PNB=90°,
由折叠的性质得:PE=BE=5,
∴EN=BN-BE=1,PN=![]() ,
,
∴BP=![]() ;
;
综上所述,BP的长是4![]() 或
或![]() 或2
或2![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目