��Ŀ����
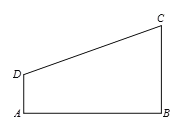
����Ŀ����ͼ1�ڷž���ֽƬABCD�����ֽƬECGF��ʹB��C��G������һ��ֱ���ϣ�CE�ڱ�CD�ϣ�����AF����MΪAF���е㣬����DM��ME.
(1)�Բ���DM��ME�Ĺ�ϵ����֤����Ľ��ۣ�
(2)����ͼ1�е�ֽƬ����������ֽƬABCD��������ֽƬECGF�������������䣬��DM��ME�Ĺ�ϵΪ______��
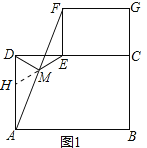
(3)��ͼ2�ڷ�������ֽƬABCD��������ֽƬECGF��ʹ��F�ڱ�CD�ϣ���M��ΪAF�ĵ㣬��DM��ME�Ĺ�ϵΪ______����˵�����ɡ�

���𰸡�DM=ME��DM��MEDM=ME��DM��ME
��������
��1���ӳ�EM��AD�ڵ�H�����á�FME�ա�AMH���ó�HM=EM��������ֱ���������У�б�ߵ����ߵ���б�ߵ�һ��֤������2���ӳ�EM��AD�ڵ�H�����á�FME�ա�AMH���ó�HM=EM��������ֱ���������У�б�ߵ����ߵ���б�ߵ�һ��֤������3������AE��AE��EC��ͬһ��ֱ���ϣ�������ֱ���������У�б�ߵ����ߵ���б�ߵ�һ��֤��.
��1��DM=ME.
֤������ͼ1���ӳ�EM��AD�ڵ�H��
���ı���ABCD��CEFG�Ǿ��Σ�
��AD��EF��
���EFM=��HAM��
�֡ߡ�FME=��AMH��FM=AM��
�ڡ�FME�͡�AMH�У�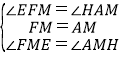 ��
��
���FME�ա�AMH��ASA��,
��HM=EM��
��RT��HDE��HM=EM��
��DM=HM=ME��
��DM=ME��
��2����ͼ1���ӳ�EM��AD�ڵ�H��
���ı���ABCD��CEFG�������Σ�
��AD��EF��
���EFM=��HAM��
�֡ߡ�FME=��AMH��FM=AM��
�ڡ�FME�͡�AMH�У�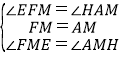 ��
��
���FME�ա�AMH��ASA��,
��HM=EM��
��RT��HDE��HM=EM��
��DM=HM=ME��
��DM=ME��
���ı���ABCD��CEFG�������Σ�
��AD=CD��CE=CF��
�ߡ�FME�ա�AMH��
��EF=AH��
��DH=DE��
���DEH�ǵ���ֱ�������Σ�
�֡�MH=ME��
��DM��ME��
�ʴ�Ϊ��DM=ME��DM��ME��
��3����ͼ2������AE��
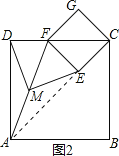
���ı���ABCD��ECGF�������Σ�
���FCE=45�㣬��FCA=45�㣬
��AE��EC��ͬһ��ֱ���ϣ�
��Rt��ADF��AM=MF��
��DM=AM=MF����MDA=��MAD��
���DMF=2��DAM��
��Rt��AEF��AM=MF��
��AM=MF=ME��
��DM=ME��
���MAE=��MEA��
���FME=2��MAE��
��֤��ADM�ա�AEM�����DAM=��EAM��
���DME=2��DAE=90�㣬
��DM��ME��
����������DM=ME��DM��ME��

 ��ҵ����ϵ�д�
��ҵ����ϵ�д� ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д�����Ŀ��������ѧϰ��һ�κ�����ʱ���۵ľ���ͷ����о�����![]() ��ͼ������ʣ���������⣮
��ͼ������ʣ���������⣮
![]() ������в��裬��������
������в��裬��������![]() ��ͼ��
��ͼ��
![]() �б�����գ�
�б�����գ�
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
![]() ��㣺
��㣺
![]() ����
����
![]() �۲�ͼ��x______ʱ��y��x�����������
�۲�ͼ��x______ʱ��y��x�����������
![]() ���ͼ����ʽ
���ͼ����ʽ![]() �Ľ⼯Ϊ______��
�Ľ⼯Ϊ______��