��Ŀ����
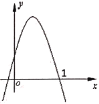
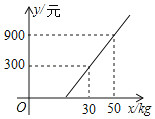
����Ŀ��ij�ÿ�Я��xkg������˷ɻ����ǻ�ǰ���ÿͿ�ѡ�����˻���������˷�y1(Ԫ)����������xkg�Ķ�Ӧ��ϵ����ͼ��ʾ��һ�κ���ͼ��ȷ�����±��г��˿�ݷ�y2(Ԫ)����������xkg�Ķ�Ӧ��ϵ��
���������xkg | ��ݷ� |
������1kg | 10Ԫ |
����1kg��������5kg�IJ��� | 3Ԫ/kg |
����5kg��������15kg�IJ��� | 5Ԫ/kg |
(1)����ÿ�ѡ�����ˣ����Я�������������������Ϊ����kg��
(2)����ÿ�ѡ���ݣ���1��x��15ʱ��ֱ��д����ݷ�y2(Ԫ)�����������xkg֮��ĺ�����ϵʽ��
(3)ij�ÿ�Я��25kg�����������mkg����(10��m��24��mΪ������)��ʣ�µ�����ѡ���ݣ���mΪ��ֵʱ���ܷ���y��ֵ��С�����������Сֵ�Ƕ���Ԫ��
���𰸡�(1)��Я�������������������Ϊ20kg��(2)y2��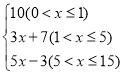 ��(3)������20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ.
��(3)������20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ.
��������
(1)�۲�ͼ���ҳ���������꣬���ô���ϵ������������˷�y1(Ԫ)����������xkg�ĺ�����ϵʽ����y1��0���뺯����ϵʽ�м��ɵó����ۣ�
(2)���ݱ����е����ݣ���x��1��1��x��5��5��x��15�������ҳ���ݷ�y2(Ԫ)����������xkg�ĺ�����ϵʽ��
(3)��10��m��20�Լ�20��m��24��������ҳ�y����m�ĺ�����ϵʽ������һ�κ��������ʿ��ҳ�y��ȡֵ��Χ���ҳ���yȡ��Сֵʱm��ֵ���ɵó����ۣ�
�⣺(1)�����˷�y1(Ԫ)����������xkg�ĺ�����ϵʽΪy1��kx+b��
��(30��300)��(50��900)����y1��kx+b��![]() ����ã�
����ã�![]() ��
��
�����˷�y1(Ԫ)����������xkg�ĺ�����ϵʽΪy1��30x��600��
��y1��30x��600��0ʱ��x��20��
�𣺿�Я�������������������Ϊ20kg��
(2)��������ã���0��x��1ʱ��y2��10��
��1��x��5ʱ��y2��10+3(x��1)��3x+7��
��5��x��15ʱ��y2��10+3��(5��1)+5(x��5)��5x��3��
������������ݷ�y2(Ԫ)����������xkg�ĺ�����ϵʽΪy2��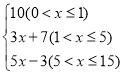 ��
��
(3)��10��m��20ʱ��5��25��m��15��
��y��y1+y2��0+5��(25��m)��3����5m+122��
��10��m��20��
��22��y��72��
��20��m��24ʱ��1��25��m��5��
��y��y1+y2��30m��600+3��(25��m)+7��27m��518��
��20��m��24��
��22��y��130��
���Ͽ�֪����m��20ʱ���ܷ���y��ֵ��С����СֵΪ22��
�𣺵�����20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ��
�ʴ�Ϊ��(1)��Я�������������������Ϊ20kg��(2)y2��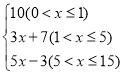 ��(3)������20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ.
��(3)������20kg�����5kg����ʱ���ܷ������٣����ٷ���Ϊ22Ԫ.

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�