题目内容
【题目】若将抛物线y=mx2﹣x﹣m(m≠0)在直线x=﹣1与直线x=1之间的部分记作图象C,对于图象C上任意一点P(a,b)均有﹣1≤b≤1成立,则m的取值范围是___.
【答案】﹣![]() ≤m≤
≤m≤![]() 且m≠0.
且m≠0.
【解析】
要使对于图象C上任意一点P(a,b)均有-1≤b≤1成立,只需在给定区域内,y的最大值都满足条件即可;分m>0和m<0两种情况讨论,当m>0时,在分①当0<![]() <1时,②当
<1时,②当![]() ≥1时;当m<0时再分①当-1<
≥1时;当m<0时再分①当-1<![]() <0时,②当
<0时,②当![]() ≤-1时,最后将解的情况综合.
≤-1时,最后将解的情况综合.
解:y=mx2﹣x﹣m (m≠0)的对称轴是x=![]() ,
,
(1)当m>0时,![]() >0,
>0,
①当0<![]() <1时,即m>
<1时,即m>![]() ,
,
此时当x=﹣1时有最大值1;
此时当x=![]() 时有最小值
时有最小值![]() ,
,
![]() =﹣1,
=﹣1,
∴m=![]() ,
,
②当![]() ≥1时,即0<m≤
≥1时,即0<m≤![]() ,
,
此时当x=﹣1时有最大值1;
此时当x=1时有最小值﹣1;
∴0<m≤![]() ;
;
(2)当m<0时,![]() <0,
<0,
①当﹣1<![]() <0时,即m<
<0时,即m<![]() ,
,
此时当x=![]() 时,y有最大值
时,y有最大值![]() ,
,
∴![]() =1,
=1,
∴m=![]() ,
,
当x=1时有最小值﹣1,
∴m=![]() ,
,
②当![]() ≤﹣1时,即
≤﹣1时,即![]() ≤m<0,
≤m<0,
此时当x=﹣1时有最大值1;
当x=1时有最小值﹣1;
∴![]() ≤m<0,
≤m<0,
综上所述,![]() ≤m≤
≤m≤![]() 且m≠0.
且m≠0.

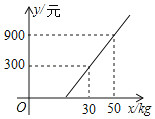
【题目】某旅客携带xkg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量xkg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量xkg的对应关系.
行李的重量xkg | 快递费 |
不超过1kg | 10元 |
超过1kg但不超过5kg的部分 | 3元/kg |
超过5kg但不超过15kg的部分 | 5元/kg |
(1)如果旅客选择单托运,求可携带的免费行李的最大重量为多少kg?
(2)如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量xkg之间的函数关系式;
(3)某旅客携带25kg的行李,设托运mkg行李(10≤m<24,m为正整数),剩下的行李选择快递,当m为何值时,总费用y的值最小?并求出其最小值是多少元?