题目内容
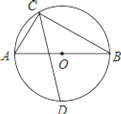
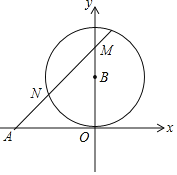
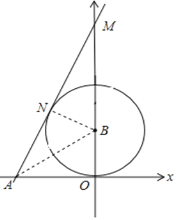
【题目】如图,已知A(﹣2,0),以B(0,1)为圆心,OB长为半径作⊙B,N是⊙B上一个动点,直线AN交y轴于M点,则△AOM面积的最大值是( )
A. 2B. ![]() C. 4D.
C. 4D. ![]()
【答案】B
【解析】
当直线AN与⊙B相切时,△AOM面积的最大.设BM=x,由切割线定理表示出MN,可证明△BNM∽△AOM,根据相似三角形的性质可求得x,然后求得△AOM面积.
解:当直线AN与⊙B相切时,△AOM面积的最大.
连接AB、BN,
在Rt△AOB和Rt△ANB中
![]()
∴Rt△AOB≌Rt△ANB,
∴AN=AO=2,
设BM=x,
∴MN2=(BM﹣1)(BM+1),
∴MN=![]() ,
,
∵∠AOM=∠BNM=90°,∠AMO=∠BMN,
∴△BNM∽△AOM,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
解得x=![]() ,
,
S△AOM=![]() =
=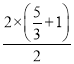 =
=![]() .
.
故选:B.

练习册系列答案
相关题目
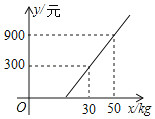
【题目】某旅客携带xkg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量xkg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量xkg的对应关系.
行李的重量xkg | 快递费 |
不超过1kg | 10元 |
超过1kg但不超过5kg的部分 | 3元/kg |
超过5kg但不超过15kg的部分 | 5元/kg |
(1)如果旅客选择单托运,求可携带的免费行李的最大重量为多少kg?
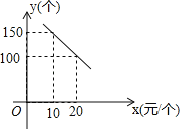
(2)如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量xkg之间的函数关系式;
(3)某旅客携带25kg的行李,设托运mkg行李(10≤m<24,m为正整数),剩下的行李选择快递,当m为何值时,总费用y的值最小?并求出其最小值是多少元?