题目内容
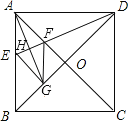
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,AG平分∠BAC交BD于G,DE⊥AG于点H.下列结论:①AD=2AE:②FD=AG;③CF=CD:④四边形FGEA是菱形;⑤OF=![]() BE,正确的有( )
BE,正确的有( )
A.2个B.3个C.4个D.5个
【答案】C
【解析】
①根据正方形的性质和角平分线的定义得:∠BAG=∠CAG=22.5°,由垂直的定义计算∠AED=90°﹣22.5°=67.5°,∠EDA=∠EDG=22.5°,得ED是AG的垂直平分线,则AE=EG,△BEG是等腰直角三角形,则AD=AB>2AE,可作判断;②证明△DAF≌△ABG(ASA),可作判断;③分别计算∠CDF=∠CFD=67.5°,可作判断;④根据对角线互相平分且垂直的四边形是菱形可作判断;⑤设BG=x,则AF=AE=x,表示OF和BE的长,可作判断.
解:①∵四边形ABCD是正方形,
∴∠BAD=90°,∠BAC=45°,
∵AG平分∠BAC,
∴∠BAG=∠CAG=22.5°,
∵AG⊥ED,
∴∠AHE=∠EHG=90°,
∴∠AED=90°﹣22.5°=67.5°,
∴∠ADE=22.5°,
∵∠ADB=45°,
∴∠EDG=22.5°=∠ADE,
∵∠AHD=∠GHD=90°,
∴∠DAG=∠DGA,
∴AD=DG,AH=GH,
∴ED是AG的垂直平分线,
∴AE=EG,
∴∠EAG=∠AGE=22.5°,
∴∠BEG=45°=∠ABG,
∴∠BGE=90°,
∴AE=EG<BE,
∴AD=AB>2AE,
故①不正确;
②∵四边形ABCD是正方形,
∴AD=AB,∠DAF=∠ABG=45°,
∵∠ADF=∠BAG=22.5°,
∴△DAF≌△ABG(ASA),
∴DF=AG,
故②正确;
③∵∠CDF=45°+22.5°=67.5°,∠CFD=∠AFE=90°﹣22.5°=67.5°,
∴∠CDF=∠CFD,
∴CF=CD,
故③正确;
④∵∠EAH=∠FAH,∠AHE=∠AHF,
∴∠AEF=∠AFE,
∴AE=AF,
∴EH=FH,
∵AH=GH,AG⊥EF,
∴四边形FGEA是菱形;
故④正确;
⑤设BG=x,则AF=AE=x,
由①知△BEG是等腰直角三角形,
∴BE=![]() x,
x,
∴AB=AE+BE=x+![]() x=(
x=(![]() +1)x,
+1)x,
∴AO=![]() =
=![]() ,
,
∴OF=AO﹣AF=![]() ﹣x=
﹣x=![]() x,
x,
∴![]() =
=![]() =
=![]() ,
,
∴OF=![]() BE;
BE;
故⑤正确;
本题正确的结论有:②③④⑤;
故选:C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案