题目内容
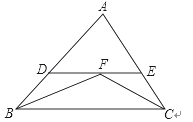
【题目】如图,在△BCE中,∠ACB=∠CAB+30°=∠ABC+60°,在边AB上取点D,在CA的延长线上取点E,使ACCE+ABBD=BC2
求证:(1)∠CEB>∠ABC;
(2)BE=2CD.
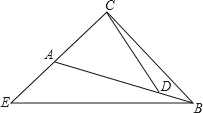
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)延长CE到F,使EF=2BD,由∠ACB=∠CAB+30°=∠ABC+60°,可得∠ACB=90°,又ACCE+ABBD=BC2,等量代换可得AC(CE+2BD)=BC2,即![]() ,则△ABC∽△BFC,∠ABC=∠F,根据三角形外角的性质,即可证得;(2)∠F=30°,则BF=2BC,易证△EFB∽△DBC,即可证得BE=2CD.
,则△ABC∽△BFC,∠ABC=∠F,根据三角形外角的性质,即可证得;(2)∠F=30°,则BF=2BC,易证△EFB∽△DBC,即可证得BE=2CD.
证明:(1)延长CE到F,使EF=2BD,
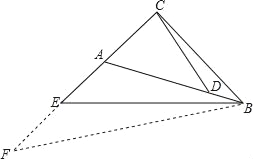
∵在△BCE中,∠ACB=∠CAB+30°=∠ABC+60°,
∴∠ACB=90°,∠ABC=30°,∠CAB=60°,
∴AB=2AC,
∵ACCE+ABBD=BC2,
∴AC(CE+2BD)=BC2,
∴AC×CF=BC2,
即![]() ,
,
∴△ABC∽△BFC,
∴∠ABC=∠F=30°,
∵∠CEB>∠F,
∴∠CEB>∠ABC;
(2)∵∠F=30°,∠FCB=90°,
∴FB=2BC,又∠F=∠CBD,EF=2BD,
∴△EFB∽△DBC,
∴![]() ,
,
∴BE=2CD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目