题目内容
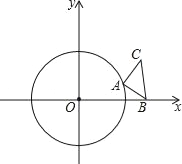
【题目】如图,⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(![]() ,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
,0),∠CAB=90°,AC=AB,顶点A在⊙O上运动.
(1)当点A在x轴的正半轴上时,直接写出点C的坐标;
(2)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O位置关系,并说明理由;
(3)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式.
【答案】(1)点A的坐标为(1,0)时,AB=AC=![]() ﹣1,点C的坐标为(1,
﹣1,点C的坐标为(1,![]() ﹣1)或(1,1﹣
﹣1)或(1,1﹣![]() );(2)见解析;(3)S==
);(2)见解析;(3)S==![]() ﹣
﹣![]() x,其中﹣1≤x≤1.
x,其中﹣1≤x≤1.
【解析】
(1)A点坐标为(1,0),根据AB=AC,分两种情形求出C点坐标;
(2)根据题意过点O作OM⊥BC于点M,求出OM的长,与半径比较得出位置关系;
(3)过点A作AE⊥OB于点E,在Rt△OAE中求AE的长,然后再在Rt△BAE中求出AB的长,进而求出面积的表达式;
(1)点A的坐标为(1,0)时,![]() ,点C的坐标为
,点C的坐标为![]() 或
或![]() ;
;
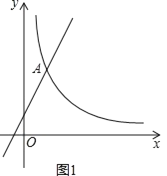
(2)如图1中,结论:直线BC与⊙O相切.理由如下:
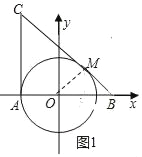
过点O作OM⊥BC于点M,
∴∠OBM=∠BOM=45°,
∴OM=OBsin45°=1
∴直线BC与⊙O相切;
(3)过点A作AE⊥OB于点E.
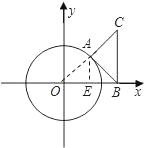
在Rt△OAE中,AE2=OA2﹣OE2=1﹣x2,
在Rt△BAE中,AB2=AE2+BE2![]() ,
,
∴![]() 其中﹣1≤x≤1.
其中﹣1≤x≤1.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目