题目内容
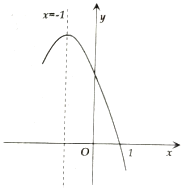
【题目】如图,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() 为抛物线上的一个动点,过点
为抛物线上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() .
.
(1)求抛物线的函数表达式和直线![]() 的解析式;
的解析式;
(2)若点![]() 在第二象限内,且
在第二象限内,且![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,若![]() 为直线
为直线![]() 上一点,是否存在点
上一点,是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]()
![]() ;
;![]() ;(2)
;(2)![]() ;(3)
;(3)
![]()
![]()
![]()
【解析】
(1)点A(2,0)、点B(-4,0),则函数的表达式为:y=a(x-2)(x+4),即可求解;把![]() 坐标代入
坐标代入![]() ,求出
,求出![]() 即可得出答案;
即可得出答案;
(2)PE=![]() OD,则PE=(
OD,则PE=(![]() x2+
x2+![]() x-2-
x-2-![]() x+2)=
x+2)=![]() (-x),求得:点D(-5,0),利用S△PBE=
(-x),求得:点D(-5,0),利用S△PBE=![]() PE×BD=
PE×BD=![]() (
(![]() x2+
x2+![]() x-2-
x-2-![]() x+2)(-4-x),即可求解;
x+2)(-4-x),即可求解;
(3)分三种情况求解即可:①当BD=BM时,②当BD=DM时,③当BM=DM时.
(1)经过![]() ,对称轴
,对称轴![]() ,
,
![]()
设解析式为![]() ,
,
![]() ,
,
∴﹣8a=﹣2
![]()
![]()
=![]()
设直线![]() ,经过
,经过![]()
![]() ..
..
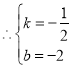
![]()
(2)设![]() ,则
,则![]()
![]()
![]()
![]() 或
或![]() .(舍)
.(舍)
![]()
=![]()
=![]()
=![]()
(3)∵直线![]() ,
,![]()
∴设M(m,![]() )
)
∵B(-4,0),D(-5,0),M(m,![]() )
)
∴![]()


当BD=BM时,即![]()
∴![]()
∴![]()
∴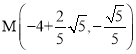 或
或
当BM=DM时,![]()
∴![]()
∴![]()
∴![]()
当BD=DM时,![]()
∴![]()
∴![]() 或
或![]() (舍去)
(舍去)
∴![]()
故答案为: ,
,![]() ,
,![]()

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.