题目内容
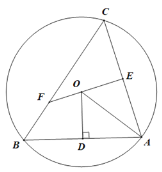
【题目】已知在![]() 中,
中,![]() .
.![]() 是
是![]() 的弦,
的弦,![]() 交
交![]() 于点
于点![]() ,且
,且![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
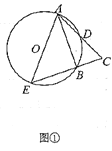
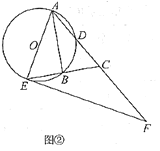
(Ⅰ)如图①,若![]() ,求
,求![]() 的大小;
的大小;
(Ⅱ)如图②,过点![]() 作
作![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的大小.
的大小.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(1)连接ED,由∠ABE=90°可得AE是⊙O的直径,根据圆周角定理可得∠ADE=∠ABE=90°,由于AD=DC,根据垂直平分线的性质可得AE=CE,则∠AED=∠CED=25°,则在直角三角形AED中,可求得∠EAD的度数;(2)首先证明三角形AEC是等边三角形,由于AB⊥CE,则易求出∠CAB的度数.
解:(Ⅰ)连接![]() .
.
![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,
![]() .
.
![]() 为
为![]() 的直径.
的直径.
![]() .
.
又![]() 为
为![]() 的中点,
的中点,
![]() 垂直平分
垂直平分![]() .
.
![]() .
.
![]() .
.
![]() .
.
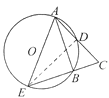
(Ⅱ)![]() 是
是![]() 的切线,
的切线,
又由(Ⅰ)得![]() 为
为![]() 的直径,
的直径,
![]() .
.
![]() .
.
![]() 为
为![]() 的中点,
的中点,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
又由(Ⅰ)得![]() ,
,
![]() .
.
![]() 是等边三角形.
是等边三角形.
![]() .
.
又![]() ,
,
![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】某学校组织健康知识竞赛,每班参加竞赛的人数相同,成绩为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,其中100分和90分为优秀.学校将八年级一班和二班的成绩整理并绘制成如下的统计图与统计表.
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,其中100分和90分为优秀.学校将八年级一班和二班的成绩整理并绘制成如下的统计图与统计表.
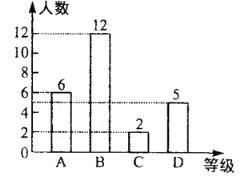
一班竞赛成绩统计图
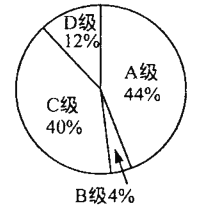
二班竞赛成绩统计图
一班和二班竞赛成绩统计表(部分空缺)
成绩 班级 | 众数 | 中位数 | 优秀率 | 平均分 |
一班 | 90 |
|
| 87.6 |
二班 |
| 80 |
|
|
请根据以上图表的信息解答下列问题:
(1)求![]() ,
,![]() ,
,![]() 的值.
的值.
(2)若全校共有750名学生参加竞赛,估计成绩优秀的学生有多少人?