Question

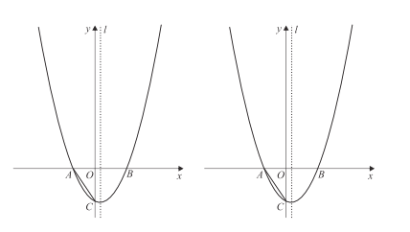
【题目】如图，矩形沿对角线折叠，点的对应点为点，连接交于点，与相交于，若，，则的长为_____________

Answer 1

【答案】1.5

【解析】

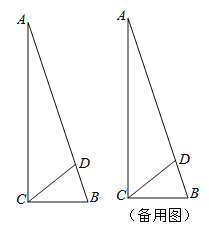
根据矩形的性质及折叠的性质，得到AD=CB=4，PB=AB=CD=2，△PGB是直角三角形等.通过证明△CGD≌△PGB得到CG=PG，设CG= PG =x，则GB=4-x，在Rt△PGB中，根据勾股定理列方程，求出CG的长即可.

解：∵四边形ABCD是矩形，，，

∴∠DAB=∠C =90°，AD=CB=4，AB=CD=2，

又∵矩形沿对角线折叠，

∴∠DPB=∠DAB=90°，PB=AB=CD=2.

在△CGD和△PGB中，

，

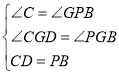∴△CGD≌△PGB（AAS），

∴CG=PG.

设CG= PG =x，则GB=4-x，

在Rt△PGB中，PG2+PB2=GB2，

即：x2+22=(4-x)2，

解得：x=1.5.

故答案为：1.5.