题目内容
【题目】综合与实践
问题情境:
小明将两个全等的![]() 和
和![]() 重叠在一起,其中
重叠在一起,其中![]() ,
,![]() ,
,![]() . 固定△DEF不动,将△ABC沿直线ED向左平移,当B与D重合时停止移动.
. 固定△DEF不动,将△ABC沿直线ED向左平移,当B与D重合时停止移动.
猜想证明:
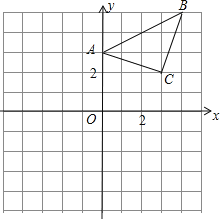
(1)如图1,在平移过程中,当点D为AB中点时,连接DC,CF,BF,请你猜想四边形CDBF的形状,并证明你的结论;

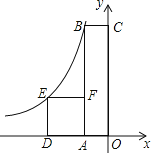
(2)如图2,在平移过程中,连接DC,CF,FB,四边形CDBF的形状在不断地变化,判断它的面积变化情况,并求出其面积;
探索发现:
(3)在平移过程中,四边形CDBF有什么共同特征?(写出两个即可)________,________;
(4)请你提出一个与△ABC平移过程有关的新的数学问题(不必证明和解答).
【答案】(1)菱形,证明见解析;(2)四边形CDBF的面积是定值![]() ;(3)①四边形CDBF的对角线互相垂直;②四边形CDBF一组对边平行;③四边形CDBF面积是一个定值.(写出两个即可,答案不唯一)(4)答案不唯一,只要符合要求即可得.如:平移过程中,求
;(3)①四边形CDBF的对角线互相垂直;②四边形CDBF一组对边平行;③四边形CDBF面积是一个定值.(写出两个即可,答案不唯一)(4)答案不唯一,只要符合要求即可得.如:平移过程中,求![]() 与
与![]() 的和.
的和.
【解析】
(1)根据平移性质证明四边形CDBF是平行四边形,再证明![]() ,问题得证;
,问题得证;
(2)过点C作![]() 于点G,求出CG,AB,根据梯形面积公式和平移性质节课求出四边形CDBF的面积;
于点G,求出CG,AB,根据梯形面积公式和平移性质节课求出四边形CDBF的面积;
(3)结合第(2)步已经平移的性质即可写出结论;
(4)根据所学知识提出一个问题即可.
(1)菱形
证明:由平移得![]() ,
,![]() ,
,
又∵点D为AB的中点,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,∴四边形CDBF是平行四边形.
,∴四边形CDBF是平行四边形.
在![]() 中,CD为中线,∴
中,CD为中线,∴![]() ,∴四边形CDBF是菱形.
,∴四边形CDBF是菱形.
(2)四边形CDBF的面积是定值.
如答图2,过点C作![]() 于点G,
于点G,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
(3)①四边形CDBF的对角线互相垂直;
②四边形CDBF一组对边平行;
③四边形CDBF面积是一个定值.
(写出两个即可,答案不唯一)
(4)答案不唯一,只要符合要求即可.如:平移过程中,求![]() 与
与![]() 的和.
的和.


【题目】经销商购进某种商品,当购进量在20千克~50千克之间(含20千克和50千克)时,每千克进价是5元;当购进量超过50千克时,每千克进价是4元.此种商品的日销售量y(千克)受销售价x(元/千克)的影响较大,该经销商试销一周后获得如下数据:
x(元/千克) | 5 | 5.5 | 6 | 6.5 | 7 |
y(千克) | 90 | 75 | 60 | 45 | 30 |
解答下列问题:
(1)求出y关于x的一次函数表达式:
(2)若每天购进的商品能够全部销售完,且当日销售价不变,日销售利润为w元,那么销售价定为多少时,该经销商销售此种商品的当日利润最大?最大利润为多少元?此时购进量应为多少千克?(注:当日利润=(销售价-进货价)×日销售量).