题目内容
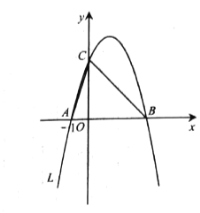
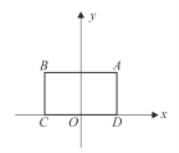
【题目】如图,抛物线![]() 与坐标轴的交点为
与坐标轴的交点为![]() ,
,![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.

(1)求抛物线的解析式.
(2)若![]() 为第二象限内一点,且四边形
为第二象限内一点,且四边形![]() 为平行四边形,求直线
为平行四边形,求直线![]() 的解析式.
的解析式.
(3)![]() 为抛物线上一动点,当
为抛物线上一动点,当![]() 的面积是
的面积是![]() 的面积的3倍时,求点
的面积的3倍时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)本题考查二次函数解析式的求法,可利用待定系数法,将点带入求解;
(2)本题考查二次函数平行四边形存在性问题,可根据题干信息结合平行四边形性质确定动点位置,进一步利用待定系数法求解一次函数解析式;
(3)本题考查二次函数与三角形面积问题,可先根据题干面积关系假设动点坐标,继而带入二次函数,列方程求解.
(1)∵抛物线![]() 与坐标轴的交点为
与坐标轴的交点为![]() ,
,![]() ,
,![]() ,
,
∴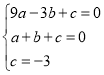 ,解得
,解得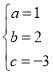
∴抛物线的解析式为![]() .
.
(2)如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
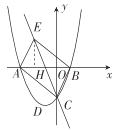
则由平行四边形的对称性可知![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() .
.
∵点![]() 的坐标为
的坐标为![]() ,
,
∴设直线![]() 的解析式为
的解析式为![]()
将点![]() 代入,得
代入,得![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(3)∵![]() ,
,
∴抛物线的顶点为![]() .
.
∵![]() 的面积是
的面积是![]() 的面积的3倍,
的面积的3倍,
∴设点![]() 为
为![]() .
.
将点![]() 代入抛物线的解析式
代入抛物线的解析式![]() 中,
中,
得![]() ,解得
,解得![]() 或
或![]() ,
,
故点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目