题目内容
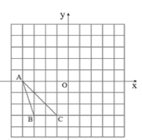
【题目】如图，在边长为1的正方形网格中，△ABC的顶点均在格点上．
(1)画出△ABC关于原点成中心对称的△A′B′C′，并直接写出△A′B′C′各顶点的坐标；
(2)连接BC′，B′C，求四边形BCB′C′的面积．
【答案】(1)见解析;(2)12.
【解析】
（1）根据中心对称的性质画出各点关于原点的对称点，顺次连接各点，并写出各点的坐标；
（2）根据题意可证明四边形
是平行四边形，再根据平行四边形的面积公式计算即可.
解：(1)如图，△A′B′C′即为所求，A′(4，0)，B′(3，3)，C′(1，3)．
(2)∵B′(3，3)，C′(1，3)，∴B′C′∥x轴，B′C′＝2，
∵B(－3，－3)，C(－1，－3)，∴BC∥x轴，BC＝2，
∴BC∥B′C′，BC＝B′C′，∴四边形BCB′C′是平行四边形，
∴SBCB′C′＝2×6＝12.
练习册系列答案
名校课堂系列答案
相关题目
