Question

【题目】如图所示，四边形ABCD是菱形，边BC在x轴上，点A（0，4），点B（3，0），双曲线y=与直线BD交于点D、点E．

（1）求k的值；

（2）求直线BD的解析式；

（3）求△CDE的面积．

Answer 1

【答案】（1）20；（2）y=2x﹣6；（3）35.

【解析】

（1）先求出D点的坐标，再代入求出即可；

（2）设直线BD的解析式为y=ax+b，把B（3，0），D（5，4）代入得出方程组，求出方程组的解即可；

（3）求出E点的坐标，分别求出△CBD和△CBE的面积，即可得出答案．

（1）∵点A（0，4），点B（3，0），

∴OA=4，OB=3，

由勾股定理得：AB=5，

过D作DF⊥x轴于F，则∠AOB=∠DFC=90°，

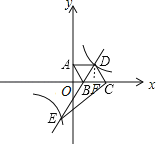
∵四边形ABCD是菱形，

∴AB=DC=CD=AD=5，AD∥BC，

∴AO=DF=4，

∵AD∥BC，AO⊥OB，DF⊥x轴，

∴∠DAO=∠AOF=∠DFO=90°，

∴四边形AOFD是矩形，

∴AD=OF=5，

∴D点的坐标为（5，4），

代入y=得：k=5×4=20；

（2）设直线BD的解析式为y=ax+b，

把B（3，0），D（5，4）代入得：，

解得：a=2，b=﹣6，

所以直线BD的解析式是y=2x﹣6；

（3）由（1）知：k=20，

所以y=，

解方程组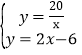得：，，

∵D点的坐标为（5，4），

∴E点的坐标为（2，10），

∵BC=5，

∴△CDE的面积S=S△CDB+S△CBE=+=35．