题目内容
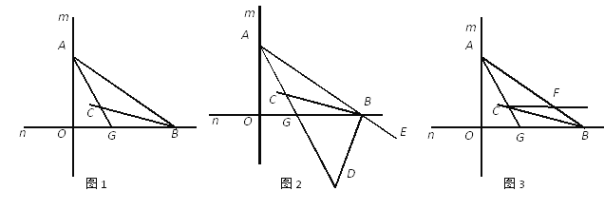
【题目】如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
(1)求∠ACB的大小;
(2)如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;
(3)如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.
【答案】(1)135°;(2)45°;(3)证明见解析.
【解析】
(1)根据角平分线的性质得到∠OAC =∠CAB,∠ABC=∠GBC,根据三角形的内角和得到∠OAB+∠ABO=90°,即可求出∠CAB+∠ABC的度数,根据三角形的内角和即可求解.
(2)根据角平分线的性质得到∠GBD=∠EBD,则∠CBD=∠GBC+∠GBD=![]() (∠ABG+∠GBE)=90°,根据∠ACB=135°即可求出∠ADB的大小.
(∠ABG+∠GBE)=90°,根据∠ACB=135°即可求出∠ADB的大小.
(3)根据三角形外角的性质得到∠AGO=∠GCB+∠GBC=45°+∠GBC,∠AGO-∠BCF=45°,可得到∠GBC=∠BCF,即可证明.
(1)∵AC、BC分别是∠BAO和∠ABO角的平分线,
∴∠OAC =∠CAB,∠ABC=∠GBC,
∵m⊥n,
∴∠AOB=90°,
∴∠ACB=180°-(∠CAB+∠ABC)
=180°-![]() (∠OAB+∠ABO)=180°-
(∠OAB+∠ABO)=180°-![]() ×90° =135°.
×90° =135°.
(2)∵BD是∠OBE角的平分线,∴∠GBD=∠EBD,
∴∠CBD=∠GBC+∠GBD=![]() (∠ABG+∠GBE)=90°,
(∠ABG+∠GBE)=90°,
又∵∠ACB=135°,∴∠DCB=45°,
∴∠ADB=180°-∠CBD -∠DCB=45°
点A、B在运动的过程中,∠ADB不发生变化,其值为45°.
(3)∵∠AGO=∠GCB+∠GBC=45°+∠GBC,
又已知:∠AGO-∠BCF=45°,
∴ 45°+∠GBC-∠BCF=45°,
∠GBC=∠BCF,∴CF∥OB.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案