Question

【题目】在Rt△ABC中，，，，CP、CM分别是AB上的高和中线，如果圆A是以点A为圆心，半径长为2的圆，那么下列判断正确的是（ ）

A. 点P，M均在圆A内 B. 点P、M均在圆A外

C. 点P在圆A内，点M在圆A外 D. 点P在圆A外，点M在圆A内

Answer 1

【答案】C

【解析】

先利用勾股定理求得AB的长，再根据面积公式求出CP的长，根据勾股定理求出AP的长，根据中线的定义求出AM的长，然后由点P、M到A点的距离判断点P、M与圆A的位置关系即可得出答案．

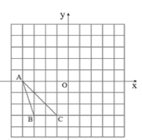
如图所示，

∵在Rt△ABC中，∠C=90°，AC=3，BC=4，

∴AB=，

∵CP、CM分别是AB上的高和中线，

∴ABCP=ACBC，AM=AB=2.5，

∴CP=2.4，

∴AP=，

∵AP=1.8<2，AM=2.5>2，

∴点P在圆A内、点M在圆A外.

故选C.