Question

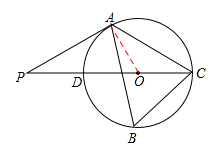
如图，△ABC内接于⊙O，∠B=60⁰，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．

（1）求证：PA是⊙O的切线；
（2）若PD=，求⊙O的直径．

Answer 1

（1）见解析（2）2

解：（1）证明：连接OA，
∵∠B=60⁰，∴∠AOC=2∠B=120⁰。
∵OA=OC，∴∠OAC=∠OCA=30⁰。
又∵AP=AC，∴∠P=∠ACP=30⁰。
∴∠OAP=∠AOC﹣∠P=90⁰。∴OA⊥PA。
∵OA是⊙O的半径，∴PA是⊙O的切线。

（2）在Rt△OAP中，∵∠P=30⁰，
∴PO=2OA=OD+PD。
又∵OA=OD，∴PD=OA。
∵PD=，∴2OA=2PD=2。
∴⊙O的直径为2。．
（1）连接OA，根据圆周角定理求出∠AOC，再由OA=OC得出∠ACO=∠OAC=30⁰，再由AP=AC得出
∠P=30⁰，继而由∠OAP=∠AOC﹣∠P，可得出OA⊥PA，从而得出结论。
（2）利用含30⁰的直角三角形的性质求出OP=2OA，可得出OP﹣PD=OD，再由PD=，可得出⊙O的直径。