题目内容
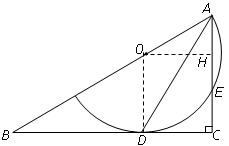
在直角三角形ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.
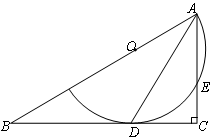
(1)求证:AD平分∠BAC;
(2)已知AE=2,DC=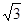 ,求圆弧的半径.
,求圆弧的半径.

(1)求证:AD平分∠BAC;
(2)已知AE=2,DC=
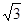 ,求圆弧的半径.
,求圆弧的半径.(1)根据切线的性质可得OD⊥BC,即得∠ODB=∠C=90°,则可得OD∥AC,根据平行线的性质可得∠ODA=∠CAD,根据圆的基本性质可得∠ODA=∠OAD,问题得证;(2)2
试题分析:(1)根据切线的性质可得OD⊥BC,即得∠ODB=∠C=90°,则可得OD∥AC,根据平行线的性质可得∠ODA=∠CAD,根据圆的基本性质可得∠ODA=∠OAD,问题得证;
(2)过O作OH⊥AC于H,根据垂径定理可得
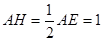 ,由OD∥AC,OH⊥AC,∠C=90°可求得OH=DC=
,由OD∥AC,OH⊥AC,∠C=90°可求得OH=DC=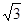 ,在Rt△ABC中,根据勾股定理即可求得结果.
,在Rt△ABC中,根据勾股定理即可求得结果.(1)∵OA为半径的圆弧与BC相切于点D
∴OD⊥BC
∴∠ODB=∠C=90°
∴OD∥AC
∴∠ODA=∠CAD
又∵OA=OD
∴∠ODA=∠OAD
∴∠CAD=∠OAD
∴AD平分∠BAC;
(2)过O作OH⊥AC于H
∴
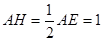
∵OD∥AC,OH⊥AC,∠C=90°,
∴OH=DC=
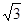
∴在Rt△ABC中,圆弧的半径OA=
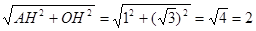 .
.点评:此类问题难度较大,在中考中比较常见,一般在压轴题中出现,需特别注意.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,求OE的长。
,求OE的长。 的中点,CD与AB的交点为E,则
的中点,CD与AB的交点为E,则 等于
等于

 cm,轴截面上有两点P、Q,PA=40cm,BQ=30cm,则圆柱的侧面上P、Q两点的最短距离是 .
cm,轴截面上有两点P、Q,PA=40cm,BQ=30cm,则圆柱的侧面上P、Q两点的最短距离是 .

 cm B.
cm B. cm D.
cm D. cm
cm 的两根,两圆圆心距为3,则两圆位置关系是( )
的两根,两圆圆心距为3,则两圆位置关系是( )