��Ŀ����
����Ŀ��������ABCD�ı߳�Ϊ4����������������ƽ��ֱ������ϵ�У�ʹAB������X����������ϣ���A��������ǣ�1��0����
��1��ֱ��![]() ������C������x�ύ���E�����ı���AECD�������
������C������x�ύ���E�����ı���AECD�������
��2����ֱ��l������E���ҽ�������ABCD�ֳ������ȵ������֣���ֱ��l�Ľ���ʽ��
��3����ֱ��l1������F����![]() ��0��������ֱ��y=3xƽ�У�����2����ֱ��l����y������ƽ��
��0��������ֱ��y=3xƽ�У�����2����ֱ��l����y������ƽ��![]() ����λ����x�ڵ�M����ֱ��l1�ڵ�N������NMF�������
����λ����x�ڵ�M����ֱ��l1�ڵ�N������NMF�������

���𰸡���1���ı���AECD�����Ϊ10����2��ֱ��l�Ľ���ʽΪy=2x-4����3��![]()
�������������������1��������֪�߳��Ѿ����ߣ������ı��ε������
��2��ֱ��l������E�ҽ�������ABCD�ֳ������ȵ������֣�����DC���ڵ�F�����������ε����ʣ������F�����꣬��ֱ��l�Ľ���ʽ��y=kx+b����E��F��������뼴���������ʽ��
��3������ֱ��l1������F����![]() ��0������ֱ��y=3xƽ�У�֪k=3����F��������뼴�����b��ֵ���ɵó�ֱ��11��ͬ���������ʽy=2x-3����һ�����M��N�����꣬���������ε������ʽ���������MNF�������
��0������ֱ��y=3xƽ�У�֪k=3����F��������뼴�����b��ֵ���ɵó�ֱ��11��ͬ���������ʽy=2x-3����һ�����M��N�����꣬���������ε������ʽ���������MNF�������
�����������1����y=![]() x
x![]() ����y=4����
����y=4����![]() x
x![]() =4����ã�x=5����B�������ǣ�5��0����
=4����ã�x=5����B�������ǣ�5��0����
��y=0����![]() x
x![]() =0����ã�x=2����E�������ǣ�2��0����
=0����ã�x=2����E�������ǣ�2��0����
��OB=5��OE=2��BE=OB��OA=5��2=3����AE=AB��BE=4��3=1��
�ı���AECD�����=![]() ��AE+CD��AD=
��AE+CD��AD=![]() ��4+1����4=10��
��4+1����4=10��
��2��������E�ҽ�������ABCD�ֳ������ȵ������֣���ֱ����CD�Ľ���F������CF=AE=1����F�������ǣ�4��4����
��ֱ�ߵĽ���ʽ��y=kx+b����![]() ����ã�
����ã� ![]() ��
��
��ֱ��l�Ľ���ʽ�ǣ�y=2x��4��
��3����ֱ��l1������F����![]() ��0������ֱ��y=3xƽ�У�
��0������ֱ��y=3xƽ�У�
��ֱ��11�Ľ���ʽ��y1=kx+b����k=3��
����ã�0=3������![]() ��+b����ã�b=
��+b����ã�b=![]() ��
��
��y1=3x+![]() ��
��
��֪����2����ֱ��l����y������ƽ��![]() ����λ�������õ�ֱ�ߵĽ���ʽ��y=2x��4+
����λ�������õ�ֱ�ߵĽ���ʽ��y=2x��4+![]() ��
��
����y=2x��3![]() ����y=0ʱ��x=
����y=0ʱ��x=![]() ����M��
����M��![]() ��0����
��0����
�ⷽ����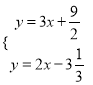 �ã�
�ã� 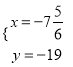 ������N����7
������N����7![]() ����19����
����19����
S��NMF=![]() ��[
��[![]() ������
������![]() ��]��|��19|=
��]��|��19|=![]() ��
��
����NMF�������![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ijУ��֯ѧ��������ѧУ6ǧ�ĿƼ���ȥ�ιۣ�С������û�ܳ���ѧУ�İ�������������ѧУ�ſڸij˳��ȥ�Ƽ��ݣ�����շѱ����������ͣ����±���
��� | �����շѣ�Ԫ�� | �����շѣ�Ԫ�� |
3ǧ�����£�����3ǧ�ף� | 7.00 | 6.00 |
3ǧ�����ϣ�ÿ����1ǧ�� | 1.60 | 1.40 |
��1��������ʻ�����Ϊxǧ�ף�![]() ��xȡ�����������ֱ�д���������͵����շѣ��ú�x�Ĵ���ʽ��ʾ����
��xȡ�����������ֱ�д���������͵����շѣ��ú�x�Ĵ���ʽ��ʾ����
��2��С�����Ͻ���11Ԫ�����˳�����Ƽ��ݳ��ѹ�������˵�����ɣ�




