题目内容
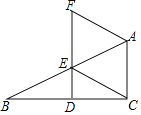
【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD于点Q,连接CQ。取CQ的中点M,连接MD,MP,若MD⊥MP,则AQ的长________。

【答案】2
【解析】分析:如图,过M作EF⊥CD于F,则EF⊥AB,证得△MDF≌△PME,求得ME=![]() ,再利用梯形的中位线定理求解即可.
,再利用梯形的中位线定理求解即可.
详解:
如图,过M作EF⊥CD于F,则EF⊥AB,

∵MD⊥MP,
∴∠PMD=90°,
∴∠PME+∠DMF=90°,
∵∠FDM+∠DMF=90°,
∴∠MDF=∠PME,
∵M是QC的中点,
根据直角三角形斜边上的中线性质求得DM=PM=![]() QC,
QC,
在△MDF和△PME中, ,
,
∴△MDF≌△PME(AAS),
∴ME=DF,PE=MF,
∵EF⊥CD,AD⊥CD,
∴EF∥AD,
∵QM=MC,
∴DF=CF=![]() DC=
DC=![]() ;
;
∴ME=![]() ,
,
∵ME是梯形ABCQ的中位线,
∴2ME=AQ+BC,即5=AQ+3,
∴AQ=2.
故答案为:2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目