题目内容
【题目】在平面直角坐标系中,正方形OABC的顶点O在原点。
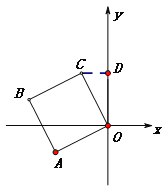
(1)如图①,点C的坐标为(![]() ,
,![]() ),且实数
),且实数![]() ,
,![]() 满足
满足![]() ,求C点的坐标及线段0C的长度;
,求C点的坐标及线段0C的长度;
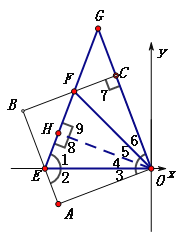
(2)如图②,点F在BC上,AB交x轴于点E,EF,OC的延长线交于点G,EG=OG,求∠EOF的度数;
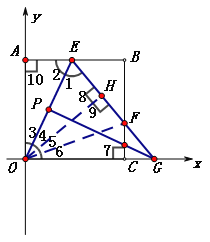
(3)如图③,将(1)中正方形OABC绕点O顺时针旋转,使OA落在y轴上,E为AB上任意一点,OE的垂直平分线交x轴于点G,交OE于点P,连接EG交BC于点F,求△BEF的周长。

【答案】(1)![]() (2)45°(3)2
(2)45°(3)2![]()
【解析】分析:(1)根据非负数的性质和二次根式有意义的条件可得b=3,a=-1,即可的点C的坐标,再由勾股定理求得OC的长;(2)过点O作OH⊥EF于H,证明△OEA≌△OEH和 Rt△OHF≌Rt△OCF,根据全等三角形的性质可得∠3=∠4,∠5=∠6,又因∠3+∠4+∠5+∠6=∠AOC=90°,即可求得∠EOF=45°;(3)过点O作OH⊥EF于H,连OF,证明△OEA≌△OEH和Rt△OHF≌Rt△OCF,根据全等三角形的性质可得AE=EH,OH=OA,HF=FC,即可得△BEF的周长=BE+EH+HF+BF=BE+AE+CF+BF=AB+BC=2![]() .
.
详解:
(1)∵b-3≥0,3-b≥0,
∴b=3,a=-1,
∴C(-1,3).
过C作CD垂直y轴于点D,则OD=3,DC=1,
∴OC=![]() ;
;
(2)过点O作OH⊥EF于H,
∵四边形OABC是正方形,
∴OA=OC,∠A=∠7=∠AOC=90°,AB∥CO,
∴∠2=∠COE又EG=OG,
∴∠1=∠COE,
∴∠1=∠2,
又OH⊥EF,
∴∠9=∠8=∠A=90°,
∴在△OEA和△OEH中,
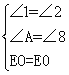 ,
,
∴△OEA≌△OEH(AAS),
∴∠3=∠4,OH=OA;
又OA=OC,
∴OH=OC,
又∠9=∠7=90°,
∴在Rt△OHF和Rt△OCF中,
![]() ,
,
∴Rt△OHF≌Rt△OCF(HL),
∴∠5=∠6,
又∠3+∠4+∠5+∠6=∠AOC=90°,
∴2∠4+2∠5=90°,
即∠4+∠5=45°,
即∠EOF=45°;
(3)过点O作OH⊥EF于H,连OF,
∵四边形OABC是正方形,
∴OA=OC,∠10=∠7=∠AOC=90°,AB∥CO,
∴∠2=∠COE又PG垂直平分OE,
∴EG=OG,
∴∠1=∠COE,
∴∠1=∠2 ,
又OH⊥EF,
∴∠9=∠8=∠10=90°,
∴在△OEA和△OEH中,

∴△OEA≌△OEH(AAS);
∴AE=EH,OH=OA,
又OA=OC,
∴OH=OC,
又∠9=∠7=90°,
∴在Rt△OHF和Rt△OCF中,
![]() ,
,
∴Rt△OHF≌Rt△OCF(HL);
∴HF=FC,
∴△BEF的周长=BE+EH+HF+BF
=BE+AE+CF+BF
=AB+BC
=2![]() .
.