题目内容
【题目】如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正确的结论有( )个. 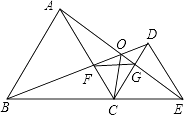
A.5
B.4
C.3
D.2
【答案】B
【解析】解:①∵△ABC和△DCE均是等边三角形, ∴BC=AC,CD=CE,∠ACB=60°,∠DCE=60°,
∴∠BCD=180°﹣60°=∠ACE.
在△BCD和△ACE中, 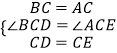 ,
,
∴△BCD≌△ACE(SAS),
∴BD=AE,结论①成立;
②∵△BCD≌△ACE,
∴∠CBF=∠CAG.
∵∠ACB=60°,∠DCE=60°,
∴∠ACG=180°﹣∠ACB﹣∠DCE=60°.
在△BCF和△ACG中, 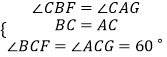 ,
,
∴△BCF≌△ACG(ASA),
∴BF=AG,结论②不成立;
③∵△BCF≌△ACG,
∴CF=CG.
∵∠FCG=60°,
∴△CFG为等边三角形,
∴∠CFG=60°.
∵∠BCF=60,
∴∠BCF=∠CFG,
∴FG∥BE,结论③成立;
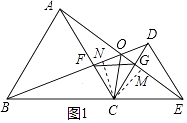
④过点C作CM⊥AE于点M,CN⊥BD于点N,如图所示.
∵△BCD≌△ACE,
∴∠CDN=∠CEM.
在△CDN和△CEM中, 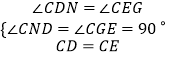 ,
,
∴△CDN≌△CEM(AAS),
∴CM=CN,
∴OC为∠BOE的角平分线,
∴∠BOC=∠EOC,结论④成立;
⑤在AE上寻找点P,连接CP使得CP=CO,如图2所示.
∵△CDN≌△CEM,
∴EM=DN,
∵BD=AE,BF=AG,
∴MG=NF.
在△CMG和△CNF中, 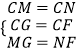 ,
,
∴△CMG≌△CNF(SSS),
∴∠MCG=∠NCF,
∴∠MCN=∠GCF=60°,
∴∠MON=360°﹣∠MCN﹣90°﹣90°=120°.
∵∠BOC=∠EOC,
∴∠BOC=∠EOC= ![]() ∠MON=60°,
∠MON=60°,
∴∠COD=180°﹣∠BOC=120°.
∵CP=CO,∠COP=60°,
∴△COP为等边三角形,
∴∠CPO=60°,OP=OC,
∴∠CPE=180°﹣∠CPO=120°=∠COD.
在△COD和△CPE中, 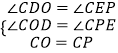 ,
,
∴△COD≌△CPE(AAS),
∴OD=PE.
∴BO=BD﹣OD=AE﹣PE=AO+OP=AO+OC,结论⑤成立.
综上所述:正确的结论有①③④⑤.
故选B.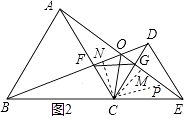
【考点精析】通过灵活运用等边三角形的性质,掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案