题目内容
【题目】已知抛物线y= 
x2﹣2x﹣1
（1）用配方法把抛物线化成顶点式，指出开口方向顶点坐标和对称轴
（2）用描点法画出图象． 
【答案】
（1）解：y= 
x2﹣2x﹣1，
= （x2﹣4x+4）﹣ ×4﹣1，
= （x﹣2）2﹣3；
∵a= ＞0，
∴开口方向：向上，
顶点坐标：（2，﹣3），
对称轴：x=2
（2）解：列表，
x | … | 0 | 1 | 2 | 3 | 4 | … |
y= | … | ﹣1 | ﹣2.5 | ﹣3 | ﹣2.5 | ﹣1 | … |
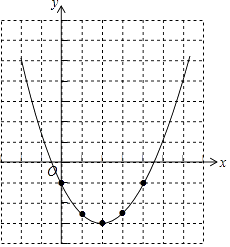
【解析】（1）根据配方法，先提取 ，然后利用完全平方公式整理即可，再根据a是正数以及顶点式形式分别求解即可；（2）根据二次函数图象的作法，列表、描点、连线画出图象即可．
【考点精析】掌握二次函数的图象是解答本题的根本，需要知道二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点．
练习册系列答案
相关题目
