题目内容
【题目】在直角坐标系xOy中,ABCD四个顶点的坐标分别为A(1,1),B(4,1),C(5,2),D(2,2),直线l:y=kx+b与直线y=﹣2x平行.
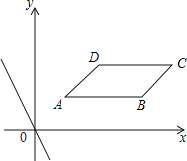
(1)k= ;
(2)若直线l过点D,求直线l的解析式;
(3)若直线l同时与边AB和CD都相交,求b的取值范围;
(4)若直线l沿线段AC从点A平移至点C,设直线l与x轴的交点为P,问是否存在一点P,使△PAB为等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)-2;(2)y=﹣2x+6;(3)3≤b≤12;(4)(![]() ,0)或(2
,0)或(2![]() +1,0)或(4﹣2
+1,0)或(4﹣2![]() ,0)
,0)
【解析】
试题分析:(1)根据平行的条件,一次项系数相同,据此即可求得;
(2)设直线l的解析式是y=﹣2x+b,把D的坐标代入解析式即可求得b的值,即可得到函数的解析式;
(3)求得经过A和C的解析式,即可求得;
(4)分成PA=PB和AP=AB和BP=BA三种情况进行讨论即可求解.
解:(1)k=﹣2;
(2)设直线l的解析式是y=﹣2x+b,
把(2,2)代入得:﹣4+b=2,解得:b=6,
则直线l的解析式是y=﹣2x+6;
(3)设过A直线l的解析式是y=﹣2x+b,把(1,1)代入得:﹣2+c=1,解得:c=3,
则直线的解析式是y=﹣2x+3,
同理,过C直线l的解析式是y=﹣2x+12,
则3≤b≤12;
(4)当直线l经过A时,解析式是y=﹣2x+3,令y=0,解得x=![]() ,即与x轴的交点是E(
,即与x轴的交点是E(![]() ,0);
,0);
当直线l经过C时,解析式是y=﹣2x+12,令y=0,解得x=6,即与x轴的交点是F(6,0);
当PA=PB时,P在AB的中垂线上,则P的坐标是(![]() ,0);
,0);
当AP=AB=3时,则PG=![]() =2
=2![]() ,则P的坐标是(2
,则P的坐标是(2![]() +1,0);
+1,0);
同理,当BP=BA=3时,P的坐标是(4﹣2![]() ,0).
,0).
故P的坐标是:(![]() ,0)或(2
,0)或(2![]() +1,0)或(4﹣2
+1,0)或(4﹣2![]() ,0).
,0).

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案【题目】如图,二次函数y1=a(x﹣2)2的图象与直线交于A(0,﹣1),B(2,0)两点.
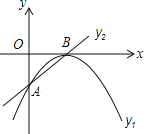
(1)确定二次函数的解析式;
(2)设直线AB解析式为y2,根据图形,确定当y1>y2时,自变量x的取值范围.
【题目】某校在一次考试中,甲,乙两班学生的数据成绩统计如下:
请根据表格提供的信息回答下列问题:
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | 甲 | 1 | 6 | 12 | 11 | 15 | 5 |
乙 | 3 | 5 | 15 | 3 | 13 | 11 | |
(1)甲班众数为 分,乙班众数为 分,从众数看成绩较好的是 班;
(2)甲班的中位数是 分,乙班的中位数是 分;
(3)若成绩在80分以上为优秀,则成绩较好的是 班;
(4)甲班的平均成绩是 分,乙班的平均成绩是 分,从平均分看成绩较好的是 班.