题目内容
【题目】(问题情境)如图,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD·AB,这个结论我们称之为射影定理,试证明这个定理;
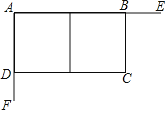
(结论运用)如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF.
(1)试利用射影定理证明△ABC∽△BED;
(2)若DE=2CE,求OF的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)可根据相似三角形的判定得到△ABC∽△BED;
(2)先计算出DE,CE,BE,OB的长度,再利用(1)中结论△ABC∽△BED结合比例性质解出OF.
(1)如图1.
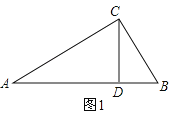
∵CD⊥AB,∴∠ADC=90°,
而∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴![]()
如图2.
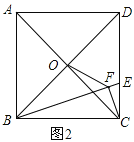
∵四边形ABCD为正方形,∴OC⊥BO,∠BCD=90°,
∴![]()
∵CF⊥BE,∴![]() ,
,
∴BOBD=BFBE,即![]() =
=![]() ,
,
而∠OBF=∠EBD,∴△BOF∽△BED;
(2)∵BC=CD=6,而DE=2CE,∴DE=4,CE=2.
在Rt△BCE中,BE=![]() =2
=2![]() .在Rt△OBC中,OB=
.在Rt△OBC中,OB=![]() BC=3
BC=3![]() .
.
∵△BOF∽△BED,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴OF=
,∴OF=![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查过程如下,请补充完整,
收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65
乙班:90,55,80,70,55,70,95,80,65,70
(1)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x人数班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=________;n=________.
(2)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 75 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=________,y=________.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀请估计乙班50名学生中身体素质为优秀的学生有________人.