题目内容
【题目】如图,AB是⊙O的直径,CD切⊙O于点D,且BD∥OC,连接AC.
(1)求证:AC是⊙O的切线;
(2)若AB=OC=4,求图中阴影部分的面积(结果保留根号和π)
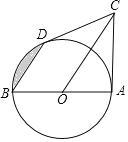
【答案】(1)证明见解析(2)![]() .
.
【解析】
(1)连接OD,根据CD与圆O相切,利用切线的性质得到OD垂直于CD,再由OC与BD平行,得到同位角相等与内错角相等,根据OB=OD,利用等边对等角得到一对角相等,等量代换得到夹角相等,再由OA=OD,OC=OC,利用SAS得到三角形AOC与三角形DOC全等,利用全等三角形对应角相等得到∠OAC=∠ODC=90°,即可得证;
(2)由OD=OB=DB得到三角形ODB为等边三角形,求出∠DOB=60°,根据图中阴影部分的面积=扇形DOB的面积-△DOB的面积解答即可.
(1)证明:连接OD,
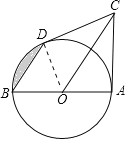
∵CD与圆O相切,
∴OD⊥CD,
∴∠CDO=90°,
∵BD∥OC,
∴∠AOC=∠OBD,∠COD=∠ODB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠AOC=∠COD,
在△AOC和△DOC中,
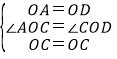 ,
,
∴△AOC≌△EOC(SAS),
∴∠CAO=∠CDO=90°,则AC与圆O相切;
(2)∵AB=OC=4,OB=OD,
∴Rt△ODC与Rt△OAC是含30°的直角三角形,
∴∠DOC=∠COA=60°,
∴∠DOB=60°,
∴△BOD为等边三角形,
图中阴影部分的面积=扇形DOB的面积-△DOB的面积=![]()
![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某课外小组的同学们在社会实践活动中调查了20户家庭莱月的用电量,如表所示:
用电量(千瓦时) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
则这20户家庭该月用电量的众数和中位数、平均数分别是( )
A. 180,160,164B. 160,180;164
C. 160,160,164D. 180,180,164