题目内容
 如图,在四边形ABCD中,AD=CD,∠D=90°,∠B=60°,AC⊥BC,点E在AC上,EC=BC,点P是CD边上一动点,若BC=4,则PA+PE的最小值等于
如图,在四边形ABCD中,AD=CD,∠D=90°,∠B=60°,AC⊥BC,点E在AC上,EC=BC,点P是CD边上一动点,若BC=4,则PA+PE的最小值等于8
8
.分析:作点E关于CD的对称点F,交CD于点G,连接AF交CD于P,连接EP,CF.由轴对称的性质可以得出CE=CF,PE=PF,证明△CGF≌△CGE就可以得出∠ECF=90°,由勾股定理就可以求出AF的值,即PA+PE的最小值.
解答:解:作点E关于CD的对称点F,交CD于点G,连接AF交CD于P,连接EP,CF
∴CE=CF,PE=PF,GE=GF.
在△CGE和△CGF中,
,
∴△CGE≌△CGF(SSS),
∴∠GCE=∠GCF.
∵AD=CD,∠D=90°,
∴∠GCE=45°,
∴∠GCF=45°,
∴∠ACF=90°.
∵BC=4,EC=BC,
∴CF=4.
∵AC⊥BC,
∴∠ACB=90°.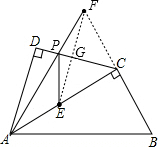
∵∠B=60°,
∴∠BAC=30°,
∴AB=2BC=8.
∵AC⊥BC,CF=BC,
∴AF=AB=8.
∵AF=AP+PF,
∴AF=AP+PE,
∴AP+PE=8
故答案为8.
∴CE=CF,PE=PF,GE=GF.
在△CGE和△CGF中,
|
∴△CGE≌△CGF(SSS),
∴∠GCE=∠GCF.
∵AD=CD,∠D=90°,
∴∠GCE=45°,
∴∠GCF=45°,
∴∠ACF=90°.
∵BC=4,EC=BC,
∴CF=4.
∵AC⊥BC,
∴∠ACB=90°.

∵∠B=60°,
∴∠BAC=30°,
∴AB=2BC=8.
∵AC⊥BC,CF=BC,
∴AF=AB=8.
∵AF=AP+PF,
∴AF=AP+PE,
∴AP+PE=8
故答案为8.
点评:本题考查了轴对称的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,最短路线问题的运用,解答时根据最短路线问题画出图形是关键.

练习册系列答案
相关题目
 (2013•赤峰)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(2013•赤峰)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD. 如图,在Rt△ABC中,∠BAC=90°,将△ABC沿线段BC向右平移得到△DEF,使CE=AE,连结AD、AE、CD,则下列结论:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四边形AECD为菱形,其中正确的共有( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC沿线段BC向右平移得到△DEF,使CE=AE,连结AD、AE、CD,则下列结论:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四边形AECD为菱形,其中正确的共有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.