题目内容
 如图,在Rt△ABC中,∠BAC=90°,将△ABC沿线段BC向右平移得到△DEF,使CE=AE,连结AD、AE、CD,则下列结论:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四边形AECD为菱形,其中正确的共有( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC沿线段BC向右平移得到△DEF,使CE=AE,连结AD、AE、CD,则下列结论:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四边形AECD为菱形,其中正确的共有( )分析:根据平移的性质得出AC∥DF,△ABC≌△DEF,根据全等三角形的性质得出BC=EF,AC=DF,∠ACB=∠F,∠B=∠DEF,根据平行线的判定推出DE∥AB,AC∥DF,得出平行四边形ACFD,推出AD=CF,即可推出各个选项.
解答:解:∵将△ABC沿线段BC向右平移得到△DEF,
∴AC∥DF,△ABC≌△DEF,
∴AC=DF,
∴四边形ACFD是平行四边形,
∴AD∥CF,AD=CF,
即AD∥AE,
∵△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF,
∴AD=BE,∴①正确;
∵△ABC≌△DEF,
∴∠ABC=∠DEF,∴②正确;
∵将△ABC沿线段BC向右平移得到△DEF,
∴AB∥ED,
∵∠BAC=90°,
即AB⊥AC,
∴ED⊥AC,∴③正确;
∵AD∥BC,
∴∠DAC=∠ACE,
∵AE=CE,
∴∠EAC=∠ACE,
∴∠DAC=∠EAC,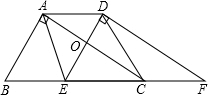
∵AC⊥DE,
∴∠AOE=∠AOD=90°,
在△ADO和△AEO中
∴△ADO≌△AEO,
∴AD=AE,
∵AE=CE,
∴AD=CE,
∵AD∥CE,
∴四边形AECD是平行四边形,
∵AE=EC,
∴四边形AECD是菱形,∴④正确;
即正确的个数是4个.
故选D.
∴AC∥DF,△ABC≌△DEF,
∴AC=DF,
∴四边形ACFD是平行四边形,
∴AD∥CF,AD=CF,
即AD∥AE,
∵△ABC≌△DEF,
∴BC=EF,
∴BC-EC=EF-EC,
∴BE=CF,
∴AD=BE,∴①正确;
∵△ABC≌△DEF,
∴∠ABC=∠DEF,∴②正确;
∵将△ABC沿线段BC向右平移得到△DEF,
∴AB∥ED,
∵∠BAC=90°,
即AB⊥AC,
∴ED⊥AC,∴③正确;
∵AD∥BC,
∴∠DAC=∠ACE,
∵AE=CE,
∴∠EAC=∠ACE,
∴∠DAC=∠EAC,

∵AC⊥DE,
∴∠AOE=∠AOD=90°,
在△ADO和△AEO中
|
∴△ADO≌△AEO,
∴AD=AE,
∵AE=CE,
∴AD=CE,
∵AD∥CE,
∴四边形AECD是平行四边形,
∵AE=EC,
∴四边形AECD是菱形,∴④正确;
即正确的个数是4个.
故选D.
点评:本题考查了平移的性质,全等三角形的性质和判定,平行四边形的性质和判定,菱形的判定,等腰三角形的性质和判定的应用,主要考查学生综合运用定理进行推理的能力.

练习册系列答案
相关题目
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离.
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,求点D到BC的距离. 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直. 如图,在Rt△ABC中,BD⊥AC,sinA=
如图,在Rt△ABC中,BD⊥AC,sinA= 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).