��Ŀ����
����Ŀ����ͼ1��һ����Ϊ2a����Ϊ2b�ij����Σ�a��b������ͼ�������ü������ȷֳ��Ŀ���ͬС�����Σ�Ȼ��ͼ2��ʽƴ��һ���������� 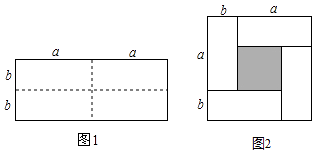
��1������Ϊͼ2�д������εı߳�Ϊ��С�����Σ���Ӱ���֣��ı߳�Ϊ �� ���ú�a��b����ʽ��ʾ��
��2����ϸ�۲�ͼ2������ͼ2�д��ڵ������ϵ��ֱ��д��������������ʽ����a��b��2 �� ��a+b��2 �� 4ab֮��ĵ�����ϵ
��3�����ã�2���еó��Ľ��۽����������⣺��֪a+b=7��ab=6�������ʽ��a��b����ֵ��
���𰸡�
��1����a+b������a��b��
��2���⣺��������ʽ֮��ĵ�����ϵ�ǣ���a+b��2=��a��b��2+4ab
��3���⣺��a��b��2=��a+b��2��4ab=25������a��b=5
���������⣺��1��ͼ2�д������εı߳�Ϊ��a+b����С�����Σ���Ӱ���֣��ı߳�Ϊ��a��b�������Դ��ǣ���a+b������a��b����

��ϰ��ϵ�д�
�����Ŀ