题目内容
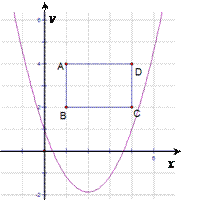
【题目】如图，二次函数
的图象经过点（0，1）坐标平面内有矩形ABCD，A（1，4），B（1，2）C（4，2），D（4，4）
（1）用a表示k；
（2）试说明抛物线图象一定经过（4,1）；
（3）求抛物线顶点在x轴上方时，a的取值范围；
（4）写出抛物线与矩形ABCD各边交点个数与a的对应取值范围.
【答案】见解析
【解析】分析：(1)把(0，1)代入抛物线解析式即可得到结论，
(2)由(1)得二次函数解析式为：
，把x=4代入即可得到结论；
(3)当抛物线顶点在x上方时，由k＞0且a≠0，解不等式即可得到结论．
(4)分五种情况讨论即可．
详解：(1)由已知把(0，1)代入
，得：
∴
．
(2)由(1)二次函数解析式可化为：
当x=4时，
∴抛物线图象一定经过（4，1）；
(3)当抛物线顶点在x上方时，>0，解得：
，
∴当且a≠0时，抛物线顶点在x轴上方．
(4)①
时，无交点；
②
时，1个交点；
③
时，2个交点；
④
时，3个交点；
⑤
时，4个交点．
练习册系列答案
计算高手系列答案
相关题目
