题目内容
【题目】如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．
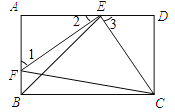
（1）求证：AE=DC；
（2）已知DC=
，求BE的长．
【答案】（1）证明见试题解析；（2）2．
【解析】
试题（1）由矩形的性质及已知条件可得到△AEF≌△DCE，即可证明AE=DC；
（2）由（1）得到AE=DC，在Rt△ABE中由勾股定理可求得BE的长．
试题解析：（1）在矩形ABCD中，∠A=∠D=90°，∴∠1+∠2=90°，∵EF⊥EC，∴∠FEC=90°，∴∠2+∠3=90°，∴∠1=∠3，在△AEF和△DCE中，∵∠A=∠D，∠1=∠3，EF=EC，∴△AEF≌△DCE（AAS），∴AE=DC；
（2）由（1）得AE=DC，∴AE=DC=
，在矩形ABCD中，AB=CD=，在R△ABE中，
，即
，∴BE=2．
练习册系列答案
相关题目
【题目】一次安全知识测验中，学生得分均为整数，满分10分，这次测验中，甲，乙两组学生人数都为5人，成绩如下（单位：分）：
甲：8，8，7，8，9
乙：5，9，7，10，9
（1）填写下表：
平均数 | 众数 | 中位数 | |
甲 | ______________ | 8 | 8 |
乙 | ______________ | 9 | ______________ |
（2）已知甲组学生成绩的方差
，计算乙组学生成绩的方差，并说明哪组学生的成绩更稳定.
