题目内容
已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.

(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
(1)证明见解析;(2)⊙O的半径是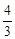 .
.
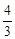 .
.试题分析:(1)连接OE,得到∠OEB =60°,从而OE∥AC.,根据平行线的性质即可得到直线EF是⊙O的切线;
(2)连接DF,DE.构造直角三角形,解直角三角形即可。
试题解析:(1)连接OE
∵△ABC是等边三角形,
∴∠ABC=∠C=60°.
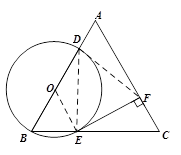
∵OB="OE,"
∴∠OEB=∠C =60°,
∴OE∥AC.
∵EF⊥AC,
∴∠EFC=90°.
∴∠OEF=∠EFC=90°.
∴OE⊥EF,
∵⊙O与BC边相交于点E,
∴E点在圆上.
∴EF是⊙O的切线;
(2)连接DF,DE.
∵DF是⊙O的切线,
∴∠ADF=∠BDF=90°
设⊙O的半径为r,则BD=2r,
∵AB=4,
∴AD=4-2r,
∵BD=2r,∠B=60°,
∴DE=
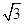 r,
r,∵∠BDE=30°,∠BDF="90°."
∴∠EDF=60°,
∵DF、EF分别是⊙O的切线,
∴DF=EF=DE=
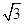 r,
r, 在Rt△ADF中,
∵∠A=60°,
∴tan∠DFA=
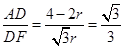
解得
 .
.∴⊙O的半径是
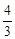

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目

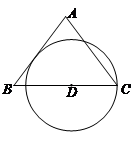
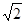 ,0),
,0),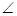 CAB="90°," AC=AB,顶点A在⊙O上运动.
CAB="90°," AC=AB,顶点A在⊙O上运动.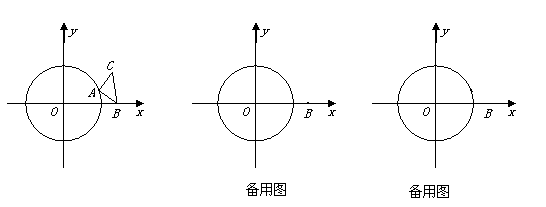



 D.
D. 
 ,∠AOB=122°,则∠AOC的度数为( )
,∠AOB=122°,则∠AOC的度数为( )
