题目内容
已知⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(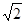 ,0),
,0), CAB="90°," AC=AB,顶点A在⊙O上运动.
CAB="90°," AC=AB,顶点A在⊙O上运动.
(1)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值;(2)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
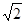 ,0),
,0),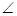 CAB="90°," AC=AB,顶点A在⊙O上运动.
CAB="90°," AC=AB,顶点A在⊙O上运动.
(1)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值;(2)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
(1)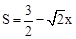 ,其中-1≤x≤1,S的最大值为
,其中-1≤x≤1,S的最大值为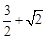 ,最小值为
,最小值为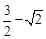 ;(2)
;(2)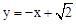 或
或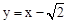 .
.
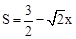 ,其中-1≤x≤1,S的最大值为
,其中-1≤x≤1,S的最大值为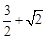 ,最小值为
,最小值为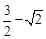 ;(2)
;(2)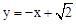 或
或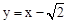 .
.试题分析:(1)过点A作AE⊥OB于点E,在Rt△OAE中求AE的长,然后再在Rt△BAE中求出AB的长,进而求出面积的表达式,结合定义域,根据一次函数的性质确定最大最小值;
(2)相切时有两种情况,在第一象限或者第四象限,连接OA,并过点A作AE⊥OB于点E,在Rt△OAE中求出OE,然后就能求出A点坐标,AB所在直线对应的函数关系式很容易就能求出.
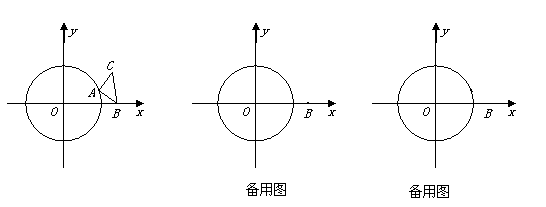
试题解析:(1)如图1,连接OA,过点A作AE⊥OB于点E,
在Rt△OAE中,
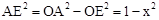 ,
,在Rt△BAE中,
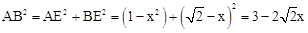 ,
,∴
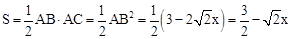 ,其中-1≤x≤1.
,其中-1≤x≤1.∴当x=-1时,S的最大值为
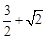 ,当x=1时,S的最小值为
,当x=1时,S的最小值为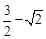 .
.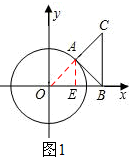
(2)①当点A位于第一象限时(如图1),连接OA,并过点A作AE⊥OB于点E,
∵直线AB与⊙O相切,∴∠OAB=90°.
又∵∠CAB=90°,∴∠CAB+∠OAB=180°.∴点O、A、C在同一条直线.
∴∠AOB=∠C=45°,即∠CBO=90°.
在Rt△OAE中,OE=AE=
 ,点A的坐标为(
,点A的坐标为( ,
, ).
).又∵B的坐标为(
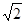 ,0),∴过A、B两点的直线为
,0),∴过A、B两点的直线为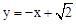 .
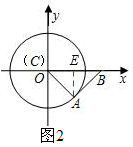
.②当点A位于第四象限时(如图2),点A的坐标为(
 ,
,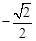 ),
),∵B的坐标为(
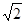 ,0),∴过A、B两点的直线为
,0),∴过A、B两点的直线为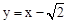 .
.综上所述,过A、B两点的直线为
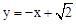 或
或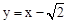 .
.
练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
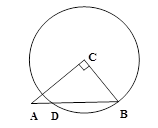
已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.

(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

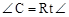 ,以顶点C为圆心,BC为半径作圆. 若
,以顶点C为圆心,BC为半径作圆. 若 .
.






 A.
A.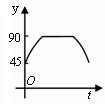 B.
B.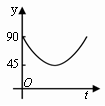 C.
C. D.
D.