题目内容
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.

(1)该三角形的外接圆的半径长等于 ;
(2)用直尺和圆规作出该三角形的内切圆(不写作法,保留作图痕迹),并求出该三角形内切圆的半径长.

(1)该三角形的外接圆的半径长等于 ;
(2)用直尺和圆规作出该三角形的内切圆(不写作法,保留作图痕迹),并求出该三角形内切圆的半径长.
(1)2.5;(2)作图见解析,该三角形内切圆的半径长为1.
试题分析:(1)根据勾股定理求出AB,即可求出答案;
(2)作两角的平分线,交点为圆心,以交点到边的距离为半径作出圆即可.根据三角形面积公式求出内切圆半径即可.
试题解析:(1)在Rt△ACB中,∠C=90°,AC=4,BC=3,由勾股定理得:
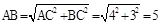
∴三角形的外接圆的半径长是
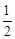 ×5=2.5.
×5=2.5.(2)作图如下:
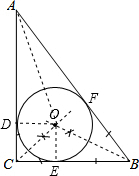
连接OA、OB、OC、OD、OE、OF,
设内切圆的半径长为r,则OD=OE=OF=r,
由S△OBC+S△OAC+S△OAB=S△ABC得:
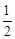 (3r+4r+5r)=
(3r+4r+5r)=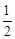 ×3×4,解得:r=1.
×3×4,解得:r=1.∴该三角形内切圆的半径长是1.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.

(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

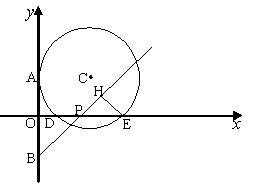

 的⊙O,E为DC的中点,连接BE,则点O到BE的距离等于 .
的⊙O,E为DC的中点,连接BE,则点O到BE的距离等于 .
 A.
A.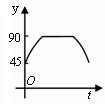 B.
B.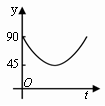 C.
C.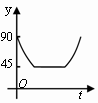 D.
D.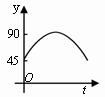
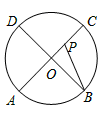
 ,若∠BEC=110°,则∠BDC( )
,若∠BEC=110°,则∠BDC( )