题目内容
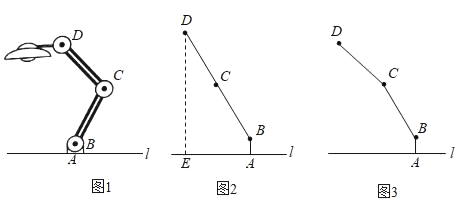
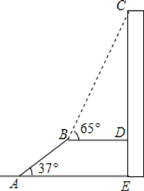
【题目】如图，AB是某火车站候车室前的自动扶梯，长为30m，坡角为37°，平台BD与大楼CE垂直，且与扶梯AB的长度相等，在B处测得大楼顶部C的仰角为65°，求大楼CE的高度．(结果精确到0.1m)（参考数据：sin37°≈
，tan37°≈
，sin65°≈
，tan65°≈
）
【答案】82.3m
【解析】
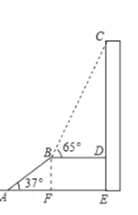
过B作BF⊥AE，再判定四边形BDEF为矩形，即可得到DE=BF；在直角三角形ABF中，利用锐角三角函数定义求出BF的长，即为DE的长；在直角三角形CBD中，利用锐角三角函数定义求出CD的长，最后CD+DE即可求出CE．
解：如图：过B作BF⊥AE，可得∠BFE=∠BDE=∠DEF=90°
∴四边形BFED为矩形。
∴DE=BF
在Rt△ABF，∠BAF=37°，AB=30m
∴BF=30×sin37=18m，即DE=18m
由题意得：BD=AB=30m
∴在Rt△BCD中，CD=30×tan65°=30×
≈64.3m
则CE=DE+CD=82.3m
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
