Question

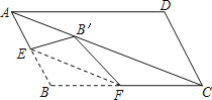
【题目】如图，直线过正方形ABCD的顶点B，点A、C到直E的距离分别是1和2，则正方形ABCD面积是____．

Answer 1

【答案】5．

【解析】

根据正方形性质得出AB=CB，∠ABC=90°，求出∠EAB=∠FBC，证△AEB≌△BFC，求出BE=CF=2，在Rt△AEB中，由勾股定理求出AB，即可求出正方形的面积．

解：如图，

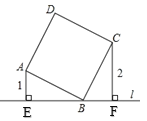
∵四边形ABCD是正方形，
∴AB=BC，∠ABC=90°，
∵AE⊥EF，CF⊥EF，
∴∠AEB=∠BFC=90°，
∴∠ABE+∠CBF=180°-90°=90°，∠ABE+∠EAB=90°，
∴∠EAB=∠CBF，
在△AEB和△BFC中，

,

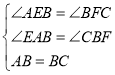∴△AEB≌△BFC（AAS），
∴BE=CF=2，
在Rt△AEB中，由勾股定理得： ,

即正方形ABCD的面积是5，
故答案为：5．