题目内容
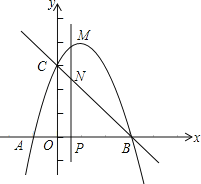
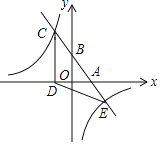
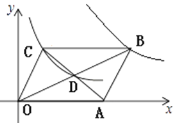
【题目】如图，在平面直角坐标系中，平行四边形OABC的对角线交于点D．双曲线
经过C，D 两点，双曲线
经过点B，则平行四边形OABC的面积为（ ）
A.4B.6C.7D.8
【答案】B
【解析】
根据平行四边形的性质得到OD=BD，设B的坐标是（2m，
），得到D的坐标是（m， 
），C的纵坐标是，求得k=m×=2，把y=代入y=
得到C的横坐标是
，根据平行四边形的面积公式即可得到结论．
解：∵平行四边形OABC的对角线交于点D，
∴OD=BD， 设B的坐标是（2m，），
∴D的坐标是（m，），C的纵坐标是，
∴k=m×=2， 把y=代入y=得：x=，
即C的横坐标是：，
∵BC=OA，
∴平行四边形OABC的面积=BC×点C的纵坐标=（2m-）×=6，
故选：B．
【题目】（2018郑州模拟）冬季即将来临，某电器超市销售每台进价分别为300元、255元的A，B两种型号的电热扇，下表是近两周的销售情况：
销售时段 | |||
销售数量 | |||
A种型号 | B种型号 | 销售收入 | |
第一周 | 2台 | 3台 | 1695元 |
第二周 | 5台 | 6台 | 3765元 |
（进价、售价均保持不变，利润
销售收入
进货成本）
（1）分别求出A，B两种型号电热扇的销售单价；
（2）若超市准备用不超过8100元的金额再采购这两种型号的电热扇共30台，求A种型号的电热扇最多能采购多少台？
（3）在（2）的条件下，超市销售完这30台电热扇能否实现利润为2100元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
【题目】复课返校后，为了让同学们进一步了解“新型冠状病毒”的防控知识，某学校组织了一次关于“新型冠状病毒”的防控知识比赛，从问卷中随机抽查了一部分，对调查结果进行了分组统计，并制作了表格与条形统计图（如图）：
分组结果 | 频数 | 频率 |
| 30 | 0.3 |
| 50 |
|
|
| 0.15 |
| 5 |
|
请根据上图完成下面题目：
（1）总人数为 人，
，
．
（2）请求出n的值并补全条形统计图．
（3）若全校有2700人，请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少？
