题目内容
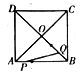
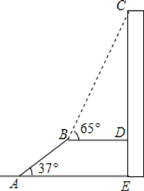
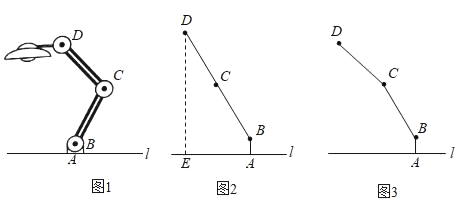
【题目】如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC、CD与AB始终在同一平面上.
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
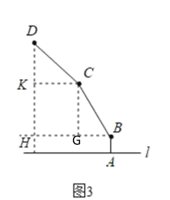
(2)将(1)中的连杆CD再绕点C逆时针旋转,经试验后发现,如图3,当∠BCD=150°时台灯光线最佳.求此时连杆端点D离桌面l的高度比原来降低了多少厘米?
【答案】(1)(20![]() +5)cm;(2)比原来降低了(10
+5)cm;(2)比原来降低了(10![]() ﹣10)厘米.
﹣10)厘米.
【解析】
(1)作BO⊥DE于O,根据矩形的判定,可得四边形ABOE是矩形,先求出∠DBO,然后根据锐角三角函数即可求出OD,从而求出DE;
(2)过C作CG⊥BH,CK⊥DE,根据锐角三角函数,即可求出CG,从而求出KH,再求出∠DCK,利用锐角三角函数即可求出DK,从而求出此时连杆端点D离桌面l的高度,即可求出结论.
解:(1)如图2中,作BO⊥DE于O.
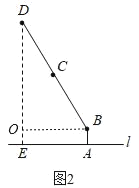
∵∠OEA=∠BOE=∠BAE=90°,
∴四边形ABOE是矩形,
∴∠OBA=90°,
∴∠DBO=150°﹣90°=60°,
∴OD=BDsin60°=20![]() (cm),
(cm),
∴DE=OD+OE=OD+AB=(20![]() +5)cm;
+5)cm;
(2)过C作CG⊥BH,CK⊥DE,
由题意得,BC=CD=20m,CG=KH,
∴在Rt△CGB中,sin∠CBH=![]() ,
,
∴CG=10![]() cm,
cm,
∴KH=10![]() cm,
cm,
∵∠BCG=90°﹣60°=30°,
∴∠DCK=150°﹣90°﹣30°=30°,
在Rt△DCK中,sin∠DCK=![]() =
=![]() =
=![]() ,
,
∴DK=10cm,
∴此时连杆端点D离桌面l的高度为10+10![]() +5=(15+10
+5=(15+10![]() )cm
)cm
∴比原来降低了(20![]() +5)﹣(15+10
+5)﹣(15+10![]() )=10
)=10![]() ﹣10,
﹣10,
答:比原来降低了(10![]() ﹣10)厘米.
﹣10)厘米.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目