题目内容
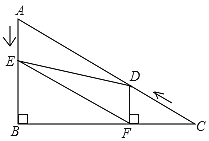
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() ,动点P从点D出发,沿线段
,动点P从点D出发,沿线段 ![]() 的方向以每秒2个单位长的速度运动;动点Q从点 C出发,在线段
的方向以每秒2个单位长的速度运动;动点Q从点 C出发,在线段 ![]() 上以每秒1个单位长的速度向点
上以每秒1个单位长的速度向点![]() 运动;点P,
运动;点P,![]() 分别从点D,C同时出发,当点
分别从点D,C同时出发,当点![]() 运动到点
运动到点 ![]() 时,点Q随之停止运动,设运动的时间为t秒).
时,点Q随之停止运动,设运动的时间为t秒).

(1)当 ![]() 时,求
时,求 ![]() 的面积;
的面积;
(2)若四边形![]() 为平行四边形,求运动时间
为平行四边形,求运动时间![]() .
.
(3)当 ![]() 为何值时,以 B、P、Q为顶点的三角形是等腰三角形?
为何值时,以 B、P、Q为顶点的三角形是等腰三角形?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)过点![]() 作
作![]() 于
于![]() ,则PM=DC,当t=2时,算出BQ,求出面积即可;(2)当四边形
,则PM=DC,当t=2时,算出BQ,求出面积即可;(2)当四边形![]() 是平行四边形时,
是平行四边形时,![]() ,即
,即![]() ,解出即可;(3)以 B、P、Q为顶点的三角形是等腰三角形,分三种情况,①
,解出即可;(3)以 B、P、Q为顶点的三角形是等腰三角形,分三种情况,①![]() ,②
,②![]() ,③
,③![]() 分别求出t即可.
分别求出t即可.
解 :(1)过点![]() 作
作![]() 于
于![]() ,则四边形
,则四边形![]() 为矩形.
为矩形.
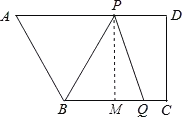
∴![]() ,
,
∵![]() ,
,
当t=2时,则BQ=14,
则![]() =
=![]() ×14×12=84;
×14×12=84;
(2)当四边形![]() 是平行四边形时,
是平行四边形时,![]() ,
,
即![]()
解得:![]()
∴当![]() 时,四边形
时,四边形![]() 是平行四边形.
是平行四边形.
(3)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分为以下三种情况:
①若![]() ,在
,在![]() 中,
中,![]() ,由
,由![]() 得
得![]() 解得:
解得:![]() ;
;
②若![]() ,在
,在![]() 中,
中,![]() ,由
,由![]() 得
得![]() ,即
,即![]() ,
,
此时,![]() ,
,
所以此方程无解,所以![]() ;
;
③若![]() ,由
,由![]() 得
得![]() ,
,
得 ![]() ,
,![]() (不合题意,舍去);
(不合题意,舍去);
综上所述,当![]() 或
或![]() 时,以B、P、Q为顶点的三角形是等腰三角形.
时,以B、P、Q为顶点的三角形是等腰三角形.

练习册系列答案
相关题目
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
|
|
|
|
|
| ··· |
![]() 可求得
可求得![]() ,第
,第![]() 个格子中的数为 ;
个格子中的数为 ;
![]() 判断:前
判断:前![]() 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为![]() 若能,求出
若能,求出![]() 的值,若不可能,请说明理由;
的值,若不可能,请说明理由;
![]() 如果
如果![]() ,
,![]() 为前
为前![]() 格子中的任意两个数,那么所有
格子中的任意两个数,那么所有![]() 的和可以通过计算
的和可以通过计算
![]() 得到,若
得到,若![]() span>,
span>,![]() 为前
为前![]() 格子中的任意两个数,则所有
格子中的任意两个数,则所有![]() 的的和为
的的和为