��Ŀ����
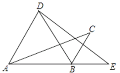
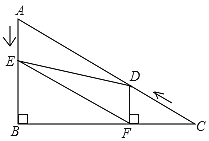
����Ŀ����ͼ����Rt��ABC�У���B=90����AC=10����C=30������D�ӵ�C������CA������ÿ��2����λ���ȵ��ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������ÿ��1����λ���ȵ��ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t��t��0���룬����D��DF��BC�ڵ�F������DE��EF��
��1����֤���ı���AEFD��ƽ���ı��Σ�
��2����tΪ��ֵʱ����DEF�ǵȱ������Σ�˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ�����ֱ��д��t��ֵ��
���𰸡���1������������2����tΪ![]() ʱ����DEF�ǵȱ������Σ�����������3����tΪ
ʱ����DEF�ǵȱ������Σ�����������3����tΪ![]() ��4ʱ����DEFΪֱ�������Σ�
��4ʱ����DEFΪֱ�������Σ�
��������
��1����Rt��CDF�У�����30�ȽǵĶԱߵ���б�ߵ�һ�룬���ɵó�DF�ij�������ý⣻
��2����֪����DEF�ǵȱ�������ʱ����EDA�ǵȱ������Σ��ɡ�A=60���ɵó�AD=AE�������ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��3����֪����DEFΪֱ��������ʱ����EDA��ֱ�������Σ��֡�AED=90���͡�ADE=90������������ǣ�����30�ȽǵĶԱߵ���б�ߵ�һ�룬�ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
�⣺��1��֤��������DFC�У���DFC=90������C=30����DC=2t��
��DF=t��
�֡�AE=t��
��AE=DF��
��AE��DF��
���ı���AEFD��ƽ���ı��Σ�
��2�����ı���AEFD��ƽ���ı��Σ�
�൱��DEF�ǵȱ�������ʱ����EDA�ǵȱ������Σ�
�ߡ�A=90��-��C=60����
��AD=AE��
��AE=t��AD=AC-CD=10-2t��
��t=10-2t��
��t=![]() ��
��
�൱tΪ![]() ʱ����DEF�ǵȱ������Σ�
ʱ����DEF�ǵȱ������Σ�
��3�����ı���AEFD��ƽ���ı��Σ�
�൱��DEFΪֱ��������ʱ����EDA��ֱ�������Σ�
����AED=90��ʱ��AD=2AE����10-2t=2t��
��ã�t=![]() ��
��
����ADE=90��ʱ��AE=2AD����t=2��10-2t����
��ã�t=4��
������������tΪ![]() ��4ʱ����DEFΪֱ�������Σ�
��4ʱ����DEFΪֱ�������Σ�