题目内容
【题目】已知:在平面直角坐标系中,点A的坐标为(m,0),点B的坐标为(0,n),其中m=![]() ,
,![]() =0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.
=0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.
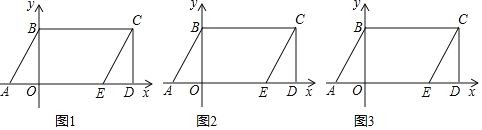
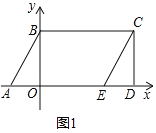
(1)如图1,分别求点C、点E的坐标;
(2)点P自点C出发,以每秒1个单位长度沿线段CB运动,同时点Q自点O出发,以每秒2个单位长度沿线段OE运动,连接AP、BQ,点Q运动至点E时,点P同时停止运动.设运动时间t(秒),三角形ABQ的面积与三角形APB的面积的和为s(平方单位),求s与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,BP:QE=8:3,此时将线段PQ向左平移2个单位长度得到线段P'Q'(点P'与点P对应),线段P′Q'再向下平移2个单位长度得到线段MN(点M与点P'对应),线段MN交x轴于点G,点H在线段OA上,OH=![]() OG,过点H作HR⊥OA,交AB于点R,求点R的坐标.
OG,过点H作HR⊥OA,交AB于点R,求点R的坐标.
【答案】(1)E(7,0),C(10,6);(2)s=3t+39(0≤t≤3.5);(3)R(﹣![]() ,
,![]() ).
).
【解析】
(1)由题意m=3,n=6,利用平移的性质解决问题即可.
(2)利用三角形的面积公式s=S△ABQ+S△ABP=![]() AQOB+
AQOB+![]() PBOB计算即可解决问题.
PBOB计算即可解决问题.
(3)利用平移的性质求出M,N的坐标,求出直线MN的解析式,可得点G的坐标,再求出点H的坐标,利用平行线分线段成比例定理构建方程求出RH即可解决问题,
(1)如图1中,
∵m=![]() ﹣
﹣![]() =2﹣5=﹣3,
=2﹣5=﹣3,![]() =0,
=0,
∴m=﹣3,n=6,
∴A(﹣3,0),B(0,6),
∵AE=BC=10,
∴OE=10﹣3=7,
∴E(7,0),C(10,6).
(2)如图2中,
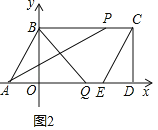
由题意:OQ=2t,PC=t,
∵OA=3,BC=10,OB=6,
∴PB=10﹣t,AQ=3+2t,
∴s=S△ABQ+S△ABP=![]() AQOB+
AQOB+![]() PBOB=
PBOB=![]() ×(3+2t)×6+
×(3+2t)×6+![]() (10﹣t)×6=3t+39(0≤t≤3.5).
(10﹣t)×6=3t+39(0≤t≤3.5).
(3)如图3中.
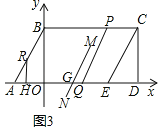
∵BP:QE=8:3,
∴(10﹣t):(7﹣2t)=8:3,
∴t=2,
∴P(8,6),Q(4,0),
∵线段PQ向左平移2个单位,再向下平移2个单位得到线段MN,
∴M(6,4),N(2,﹣2),
设直线MN的解析式为y=kx+b
把M(6,4),N(2,﹣2)代入得![]()
解得
∴直线MN的解析式为y=![]() x﹣5,
x﹣5,
令y=0,得到x=![]() ,
,
∴G(![]() ,0),
,0),
∵OH=![]() OG,
OG,
∴OH=![]() ,AH=3﹣
,AH=3﹣![]() =
=![]() ,
,
∵HR⊥OA,
∴RH∥OB,
∴![]() ,
,
∴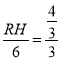 ,
,
∴RH=![]() ,
,
∴R(﹣![]() ,
,![]() ).
).

 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案