题目内容
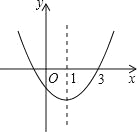
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
下列结论：
（1）ac＜0； （2）当x＞1时，y的值随x值的增大而减小．
（3）3是方程ax2+（b-1）x+c=0的一个根；（4）当-1＜x＜3时，ax2+（b-1）x+c＞0．
其中正确的的是_________；（填序号）
【答案】（1）、（3）、（4）．
【解析】
试题解析：由图表中数据可得出：x=1时，y=5值最大，所以二次函数y=ax2+bx+c开口向下，a＜0；又x=0时，y=3，所以c=3＞0，所以ac＜0，故（1）正确；
∵二次函数y=ax2+bx+c开口向下，且对称轴为x=
=1.5，∴当x＞1.5时，y的值随x值的增大而减小，故（2）错误；
∵x=3时，y=3，∴9a+3b+c=3，∵c=3，∴9a+3b+3=3，∴9a+3b=0，
∴9a+3b-3+3=0，
∴3是方程ax2+（b-1）x+c=0的一个根，故（3）正确；
∵x=-1时，ax2+bx+c=-1，∴x=-1时，ax2+（b-1）x+c=0，∵x=3时，ax2+（b-1）x+c=0，且函数有最大值，∴当-1＜x＜3时，ax2=（b-1）x+c＞0，故（4）正确．
故答案为：（1）、（3）、（4）．
练习册系列答案
相关题目
