题目内容

【题目】已知二次函数y1＝ax2+bx+c（a＞0）与一次函数y2＝kx+m的图象相交于A（﹣1，4）、B（4，2）两点，则能使关于x的不等式ax2+（b﹣k）x+c﹣m＞0成立的x的取值范围是（　　）

A.2＜x＜4B.﹣1＜x＜4C.x＜﹣1或x＞4D.x＞4

【答案】C

【解析】

根据题意得出当ax2+bx+c＞kx+m时，则ax2+（b-k）x+c-m＞0，进而结合函数图象得出x的取值范围．

解：如图，

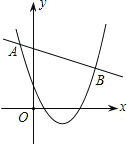
∵当ax2+bx+c＞kx+m时，

∴ax2+（b﹣k）x+c﹣m＞0，

即y1＞y2时，由二次函数y1＝ax2+bx+c与一次函数y2＝kx+m的图象相交于A（﹣1，4）、B（4，2）两点，

则由图象可得出：x＜﹣1或x＞4．

故选：C．

练习册系列答案
相关题目

【题目】教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热到100℃停止加热，水温开始下降，此时水温（℃）与开机后用时（）成反比例关系，直至水温降至30℃，饮水机关机，饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时接通电源，水温（℃）与时间（）的关系如图所示：

（1）分别写出水温上升和下降阶段与之间的函数关系式；

（2）怡萱同学想喝高于50℃的水，请问她最多需要等待多长时间？

【题目】（10分）水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售．

（1）若将这种水果每斤的售价降低x元，则每天的销售量是 斤（用含x的代数式表示）；

（2）销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？

【题目】（发现）x4﹣5x2+4＝0是一个一元四次方程．

（探索）根据该方程的特点，通常用“换元法”解方程：

设x2＝y，那么x4＝　 　，于是原方程可变为　 　．

解得：y1＝1，y2＝　 　．

当y＝1时，x2＝1，∴x＝±1；

当y＝　 　时，x2＝　 　，∴x＝　 　；

原方程有4个根，分别是　 　．

（应用）仿照上面的解题过程，求解方程：（x2﹣2x）2+（x2﹣2x）﹣6＝0

【题目】如图，在平面坐标系xOy中，点A的坐标为（1，0），点P的横坐标为2，将点A绕点P旋转，使它的对应点B恰好落在x轴上（不与A点重合）；再将点B绕点O逆时针旋转90°得到点C．

（1）直接写出点B和点C的坐标；

（2）求经过A，B，C三点的抛物线的表达式．

【题目】已知关于x的二次函数y＝2x2+bx+c．当x＝1时，y＝4；当x＝﹣2，y＝﹣5．

（1）求y关于x的二次函数的解析式；

（2）在直角坐标系中把（1）中的图象抛物线平移到顶点与原点重合，应该怎样平移？

【题目】如图，四边形内接于⊙，是⊙的直径，过点作，交的延长线于点，平分.

(1)求证:是⊙的切线;

(2)已知cm，cm，求⊙的半径.

【题目】我市茶叶专卖店销售某品牌茶叶，其进价为每千克 240 元，按每千克 400 元出售，平均每周可售出 200 千克，后来经过市场调查发现，单价每降低 10 元，则平均每周的销售量可增加 40 千克，若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元，请回答：

（1）每千克茶叶应降价多少元？

（2）在平均每周获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的 几折出售？

【题目】如图，有一座拱桥是圆弧形，它的跨度AB=60米，拱高PD=18米．

（1）求圆弧所在的圆的半径r的长；

（2）当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE=4米时，是否要采取紧急措施？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网