题目内容
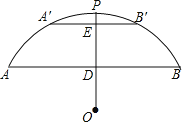
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
【答案】(1)r=34;(2)不需要采取紧急措施.
【解析】试题分析:(1)连结OA,利用r表示出OD的长,在Rt△AOD中根据勾股定理求出r的值即可;
(2)连结OA′,在Rt△A′EO中,由勾股定理得出A′E的长,进而可得出A′B′的长,据此可得出结论.
试题解析:(1)连结OA,
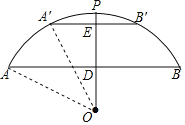
由题意得:AD=![]() AB=30,OD=(r-18)
AB=30,OD=(r-18)
在Rt△ADO中,由勾股定理得:r2=302+(r-18)2,
解得,r=34;
(2)连结OA′,
∵OE=OP-PE=30,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2-OE2,即:A′E2=342-302,
解得:A′E=16.
∴A′B′=32.
∵A′B′=32>30,
∴不需要采取紧急措施.

练习册系列答案
相关题目