Question

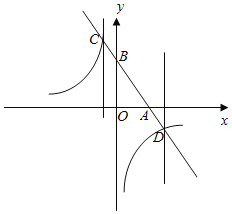
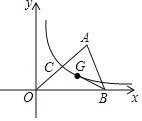
【题目】如图，在平面直角坐标系中，O为坐标原点，点A在第一象限，点B在x轴的正半轴上，点G为△OAB的重心，连接BG并延长，交OA于点C，反比例函数y＝（k＞0）的图象经过C，G两点．若△AOB的面积为6，则k的值为（　　）

A.B.C.D.3

Answer 1

【答案】B

【解析】

过点C作CN⊥OB于N，GM⊥OB于M，如图，利用三角形重心性质得BG=2CG，再根据平行线分线段成比例定理得到=，则可设GM=2a，则CN=3a，所以G(，2a)，C(，3a)，接着利用BM：BN=2：3得到BN=，然后根据S△OBC=S△OAB，列式求解．

解：过点C作CN⊥OB于N，GM⊥OB于M，如图，

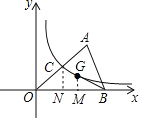
∵点G为△OAB的重心，

∴BG=2CG，

∵GM∥CN，

∴===，

设GM=2a，则CN=3a，

∴G(，2a)，C(，3a)，

∵BM：BN=2：3，

∴BN=3MN=3()=，

∴OB=ON+BN==，

∵BC为△OAB的中线，

∴S△OBC=S△OAB=×6=3，

即×3a×=3，

∴k=．

故选：B．