题目内容
【题目】在![]() 中,
中,![]() ,CD是中线,
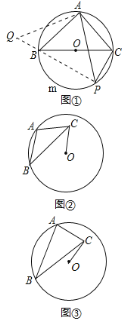
,CD是中线,![]() ,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E、F,DF与AE交于点M,DE与BC交于点N.
,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E、F,DF与AE交于点M,DE与BC交于点N.
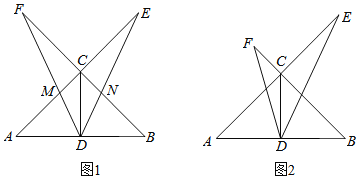
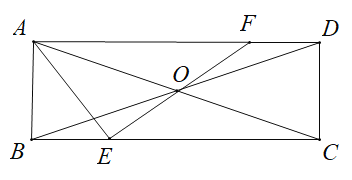
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
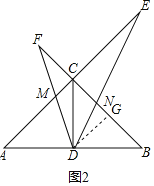
(2)如图2,在![]() 绕点D旋转的过程中,试证明
绕点D旋转的过程中,试证明![]() 恒成立;
恒成立;
(3)若![]() ,
,![]() ,求DN的长.
,求DN的长.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)根据等腰直角三角形的性质得到∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,于是得到∠DCE=∠DCF=135°,根据全等三角形的性质即可的结论;
(2)证得△CDF∽△CED,根据相似三角形的性质得到![]() ,即CD2=CECF;
,即CD2=CECF;
(3)如图,过D作DG⊥BC于G,于是得到∠DGN=∠ECN=90°,CG=DG,当CD=2,![]() 时,求得
时,求得![]() ,再推出△CEN∽△GDN,根据相似三角形的性质得到
,再推出△CEN∽△GDN,根据相似三角形的性质得到![]() ,求出GN,再根据勾股定理即可得到结论.
,求出GN,再根据勾股定理即可得到结论.
(1)证明:∵![]() ,
,![]() ,CD是中线,
,CD是中线,
∴![]() ,
,![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,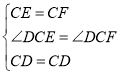 ,
,
∴![]() .
.
∴![]() ;
;
(2)证明:∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,即
,即![]() .
.
(3)如图,过D作![]() 于点G,
于点G,
则![]() ,
,![]() .
.
当![]() ,
,![]() 时,
时,
由![]() ,得
,得![]() .
.
在![]() 中,
中,
![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴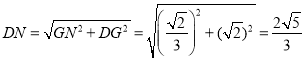 .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】官渡区某校八年级(1)班同学为了解某市2019年![]() 小区家庭月均用水情况,随机调查了该小区都分家庭,并将调查数据进行如下整理:
小区家庭月均用水情况,随机调查了该小区都分家庭,并将调查数据进行如下整理:
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 |
|
| 2 | 0.04 |
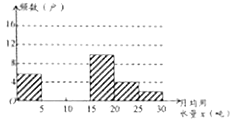
请解答下列问题:
(1)填空:样本容量是______,![]() ______,
______,![]() _______;
_______;
(2)把频数分布直方图补充完整;
(3)若该小区有1000户家庭,请估计该小区月均用水量满足![]() 的家庭有多少户?
的家庭有多少户?